题目描述

译自 ROI 2021 Day2 T2. Гаджеты на дереве

瓦西娅最近想出了一个新游戏。给定一个连通的有向图，包含 $n$ 个顶点和 $2 \cdot (n - 1)$ 条边，并且对于每条边 $(u, v)$，存在一条边 $(v, u)$。换句话说，这个图是从一棵树中得到的，其中每条边被分解成两个方向相反的边。

我们称一对边 $(e_1, e_2)$ 为一个配对，如果 $e_1$ 的终点与 $e_2$ 的起点相同，反之亦然（特别地，两条相反的边是一个配对）。瓦西娅的游戏是将图中的边分成不相交的配对。当然，他很容易就能做到这一点。

瓦西娅的朋友彼得从树中删除了 $2 \cdot k$ 条有向边。因此，图中剩下 $m = 2 \cdot (n - 1) - 2 \cdot k$ 条有向边。

现在瓦西娅想知道，是否可以将剩下的边分成不相交的配对，如果可以，请找到这种分法。请帮助他！

输入格式

第一行包含两个整数 $n, m\ (2 \le n \le 1.5\cdot 10^5, 2 \le m \le 2n-2)$，表示顶点数和剩余边数。保证 $m$ 是偶数。

接下来的 $m$ 行，每行包含两个整数 $u_i, v_i$ ($1 \le u_i, v_i \le n$)，表示剩余边的起点和终点。

输出格式

如果不能将边分成配对，输出 No。

否则，输出 Yes，然后输出 $\frac{m}{2}$ 行，每行包含 $4$ 个整数，表示每个配对中的两条边。每条边用起点和终点两个数表示。

5 6
1 2
2 1
1 5
2 3
2 4
4 2

Yes
1 2 2 3
2 1 1 5
2 4 4 2

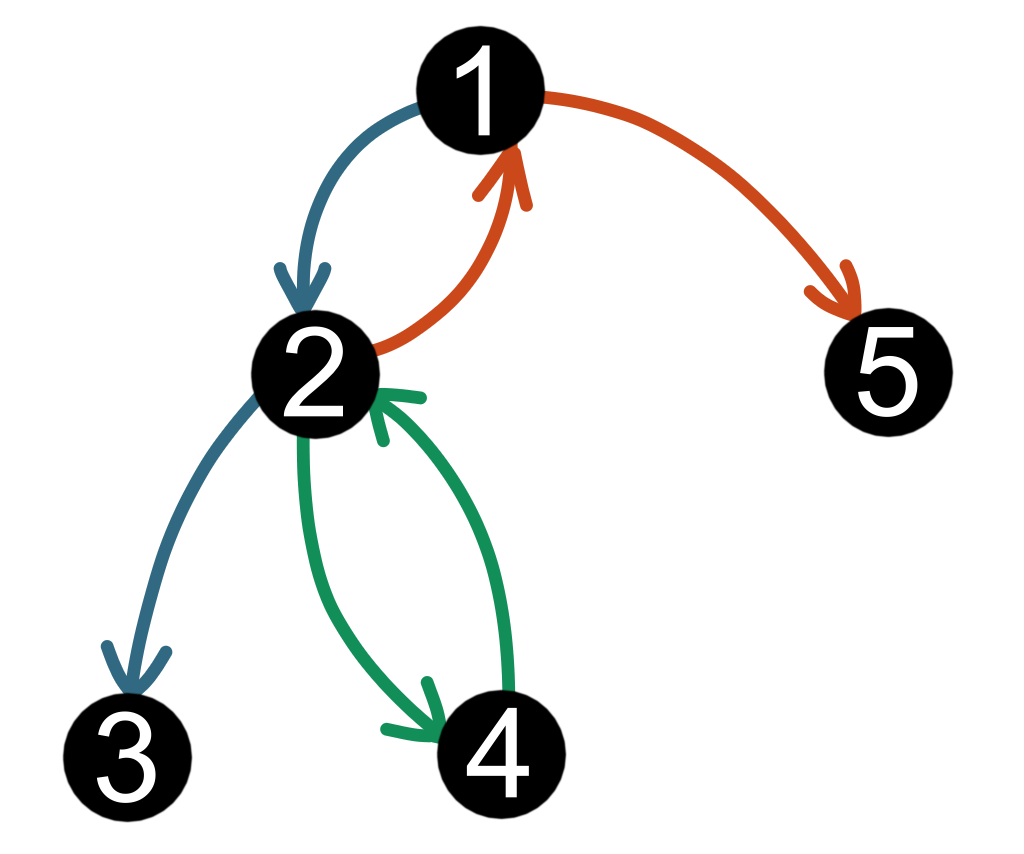
第一个示例中的配对分法如图所示。

4 4
2 1
2 3
2 4
4 2

No

4 4
1 2
2 1
3 4
4 3

Yes
1 2 2 1
3 4 4 3

数据范围与提示

详细子任务附加限制及分值如下表所示。其中子任务 $0$ 是样例。