注意事项

在 LibreOJ 上，由于语言限制，目前只支持以下语言的提交：

• C++（标准为 C++ 17 及以上）

请在提交源代码前添加 #include "train.h"。

题目描述

题目译自 2020년도 국제정보올림피아드 대표학생 선발고사 - 2차 선발고사 T3 「열차의 이동」

调车场是连接或分离列车车厢并进行维护和保养的地方。调车场中有可以移动列车的轨道。我们将用图来表示轨道上列车车厢的位置。图中的每条边表示列车的一个车厢所在的位置，因此列车在图中表示为一条路径。在这条路径上，所有的顶点和边都必须不同。特别地，问题中给出的图总是树形结构。

列车可以沿着轨道移动。列车的移动是分阶段进行的，每个阶段列车的一端车厢移动到相邻的另一条边上。具体来说，对于表示列车的路径 $P$，一次移动的结果是将 $P$ 的一端顶点和相邻的 $P$ 之外的边和顶点添加到 $P$ 中，并将另一端的顶点和边从 $P$ 中移除（见图 1）。注意，每个阶段路径的长度保持不变。

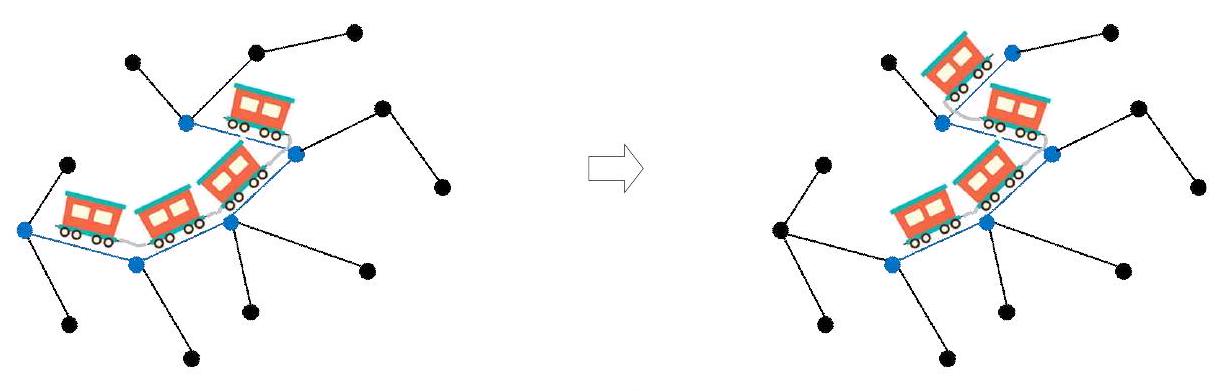
给定初始和最终列车位置的长度为 $m$ 的路径 $P$ 和 $Q$。路径的长度是路径中包含的边的数量。这里，路径 $P$ 和 $Q$ 之间没有任何共享的边。换句话说，$P$ 和 $Q$ 没有同时经过的边。我们需要将路径 $P$ 移动到最终成为路径 $Q$。此时，需要找到最少的移动步数。

给定包含 $n$ 个顶点的树 $T$ 以及初始和最终列车位置的长度为 $m$ 的路径 $P$ 和 $Q$，编写一个程序，检查是否可以将 $P$ 移动到 $Q$，如果可以，输出最少的移动步数。

例如，在图 2 中，给定长度为 $2$ 的两个路径 $P$ 和 $Q$，它们没有任何共享的边。可以看到，从路径 $P$ 移动到路径 $Q$ 需要 $5$ 步，这是最少的移动步数。

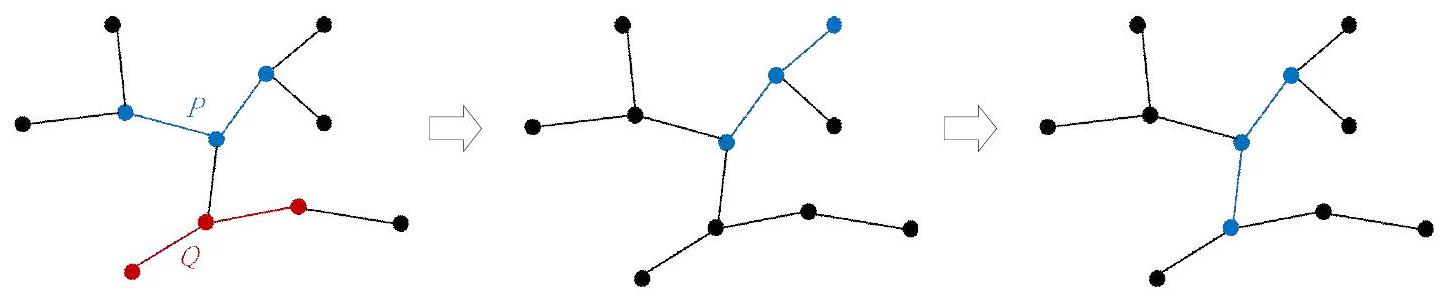
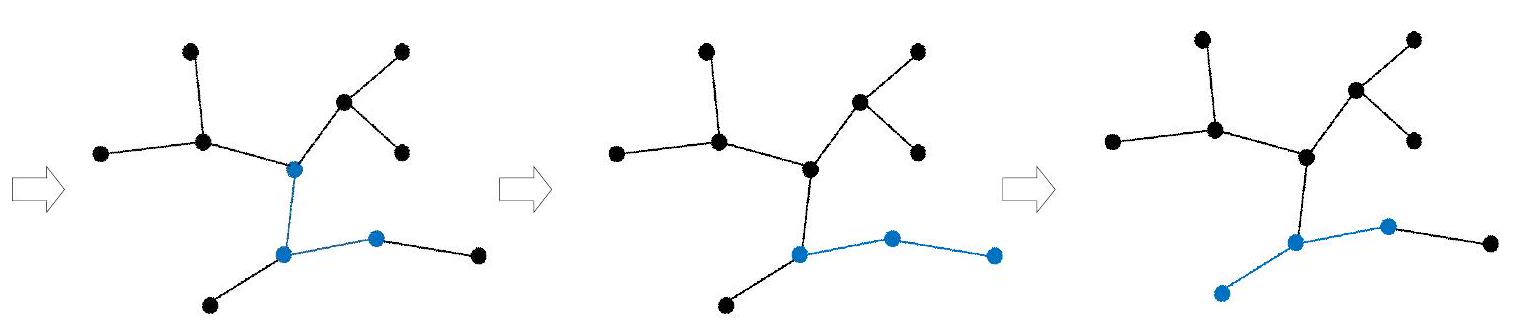
你需要为管理员实现以下两个函数：

void init(int n, vector<int> X, vector<int> Y);

• 该函数在程序开始时调用一次。树的顶点数量为 $n$，顶点编号从 $1$ 到 $n$。X 和 Y 是大小为 $n-1$ 的 vector，表示树的每条边为 $(X[i], Y[i])$。

long long train(vector<int> Z);

• 参数 Z 是大小为 $4$ 的 vector，表示初始路径 $P$ 的两个端点 Z[0] 和 Z[1]，以及最终路径 $Q$ 的两个端点 Z[2] 和 Z[3]。函数返回将 $P$ 移动到 $Q$ 的最少步骤数。如果无法移动，则返回 -1。

实现细节

你需要提交一个名为 train.cpp 的文件，该文件中实现以下两个函数：

void init(int n, vector<int> X, vector<int> Y);
long long train(vector<int> Z);

这些函数应按照上述描述工作。当然，你可以创建其他函数并在内部使用。提交的代码不应执行输入输出操作或访问其他文件。

示例评测程序

评测程序按以下格式读取输入：

• 第 $1$ 行：$n\,q$，$n$ 表示树的顶点数量，树的顶点编号从 $1$ 到 $n$，$q$ 表示查询的数量
• 接下来的 $n-1$ 行：$x\,y$，表示树的一条边 $(x, y)$，1 ≤ x ≠ y ≤ n
• 接下来的 $q$ 行：$a\,b\,c\,d$，表示初始路径 $P$ 的两个端点 $a$ 和 $b$，最终路径 $Q$ 的两个端点 $c$ 和 $d$）

评测程序将输出函数 train 的返回值。如果无法移动，则输出 -1。

11 2
1 2
3 2
4 3
4 5
6 5
8 4
7 8
8 9
10 9
11 10
3 5 7 4
3 6 7 10

3
7

以下是样例中函数调用及其结果的顺序：

数据范围与提示

对于所有输入数据，满足：

• $3 \leq n \leq 2.5\cdot 10^5$
• $1 \leq q \leq 2.5\cdot 10^5$
• 所有查询中路径 $P$ 的长度总和 $\leq 10^6$

详细子任务附加限制及分值如下表所示。