题目描述
译自 ROI Regional 2022 Day2 T3. Оптические каналы связи
在弗拉特兰有 n 个城市,编号从 1 到 n,其中首都的编号为 1。弗拉特兰的计算机网络结构如下:每个城市都有一个连接中心,可以通过有线通信渠道与其他一些中心相连。任意两个城市之间只有一条路径连接,也就是说,这个网络是一个树形结构。对于编号为 i (i>1) 的城市,从城市 i 到首都的路径上的第一个城市记为 pi。
计划对弗拉特兰的网络进行升级,将一些有线通信渠道替换为更先进的光纤通信渠道。光纤渠道只能替换现有的有线渠道。将连接城市 i 和城市 pi 的渠道替换为光纤的成本为 wi。由于技术限制,任何连接中心最多只能通过光纤渠道连接到 k 个其他中心。
弗拉特兰的通信部希望制定一个升级计划,使得升级后的光纤网络的连通性尽可能高。因此,需要选择尽可能多的渠道进行升级。同时,为了尽量减少升级成本,在数量相同的情况下,应选择总成本最小的渠道进行升级。
请帮助通信部的专家选择要升级的渠道。
输入格式
第一行包含两个整数 n 和 k (2≤n≤105,1≤k≤100)。
接下来的 n−1 行描述了渠道,第 (i−1) 行包含两个整数:pi 和 wi (1≤pi≤i,0≤wi≤109)。
输出格式
输出两个整数 cnt 和 cost,表示可以升级的最大渠道数量以及升级这些渠道的最小成本。
8 2
1 0
1 0
1 0
2 0
2 0
2 0
1 0
4 0
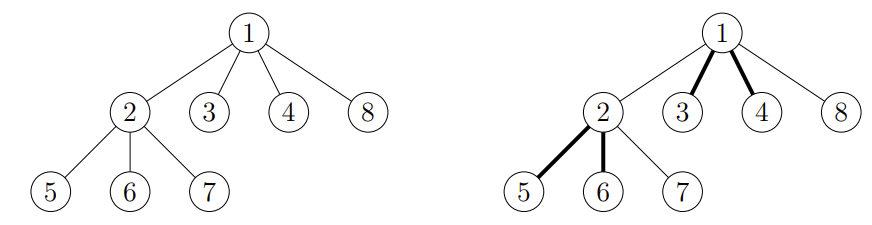
样例 1 中,网络在升级前后的配置如下图所示。需要升级的渠道用粗线表示。可以升级的最大渠道数量为 4。任何渠道的升级成本均为 0,因此未显示。
还有其他合适的方案,可以升级 4 个渠道。
8 3
1 5
1 2
1 4
2 6
2 7
2 2
1 6
6 27
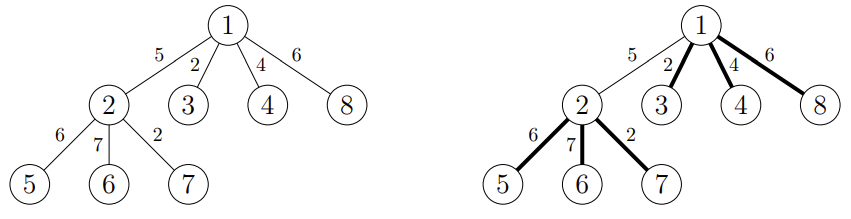
样例 2 中,网络在升级前后的配置如下图所示。需要升级的渠道用粗线表示。可以升级的最大渠道数量为 6。每个渠道的升级成本显示在渠道旁边,最优方案的总升级成本为 27。
数据范围与提示
详细子任务附加限制及分值如下表所示。
| 子任务 |
分值 |
附加限制 |
子任务依赖 |
| 1 |
5 |
n≤15,k=1,wi=0 |
无 |
| 2 |
n≤15,wi=0 |
1 |
| 3 |
3 |
n≤15 |
1,2 |
| 4 |
7 |
k=1,wi=0 |
1 |
| 5 |
5 |
k=1 |
1,4 |
| 6 |
7 |
k≤2,wi=0 |
1,4,5 |
| 7 |
4 |
k≤2 |
1,4,5,6 |
| 8 |
11 |
n≤100,wi=0 |
1,2 |
| 9 |
4 |
n≤100 |
1,2,3,8 |
| 10 |
11 |
n≤2000,wi=0 |
1,2,8 |
| 11 |
4 |
n≤2000 |
1,2,3,8,9,10 |
| 12 |
20 |
wi=0 |
1,2,4,6,8,10 |
| 13 |
14 |
无 |
1∼12 |

