题目描述
译自 ROI Regional 2023 Day1 T4. Разноцветные точки
我们来看平面上的 n n n 1 1 1 n n n P 1 , P 2 , … , P n P_{1}, P_{2}, \ldots, P_{n} P 1 , P 2 , … , P n i i i ( x i , y i ) \left(x_{i}, y_{i}\right) ( x i , y i )
考虑以下过程。选择一个起始点 i i i j j j ( i ≠ j ) (i \neq j) ( i = j ) t t t k k k P i P_{i} P i P j P_{j} P j P i P j → \overrightarrow{P_{i} P_{j}} P i P j j j j P i P j → \overrightarrow{P_{i} P_{j}} P i P j j j j k k k t t t j j j k k k
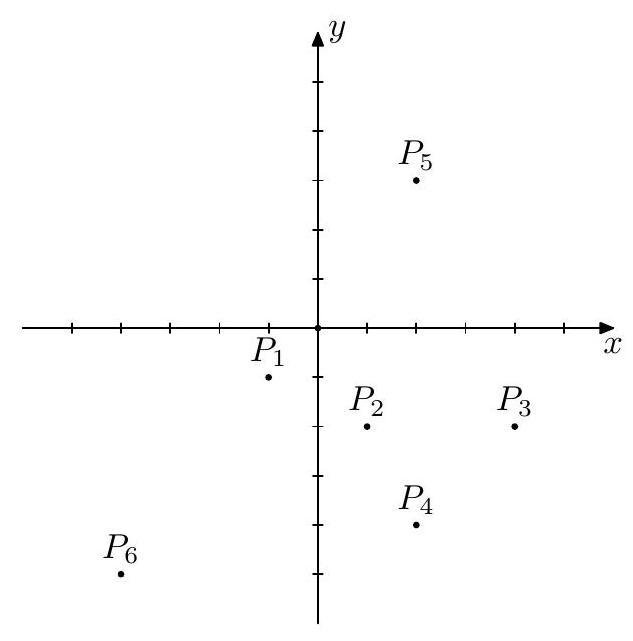
为了更好地理解这个过程,我们来看一个例子。假设有 6 6 6 t = 4 t=4 t = 4 1 1 1 2 2 2 P 2 P_{2} P 2 P 1 P 2 → \overrightarrow{P_{1} P_{2}} P 1 P 2 P 2 P_{2} P 2 P 1 P 2 → \overrightarrow{P_{1} P_{2}} P 1 P 2 P 2 P_{2} P 2
图 1:6 个点的例子 \text{图 1:6 个点的例子}
图 1 : 6 个点的例子
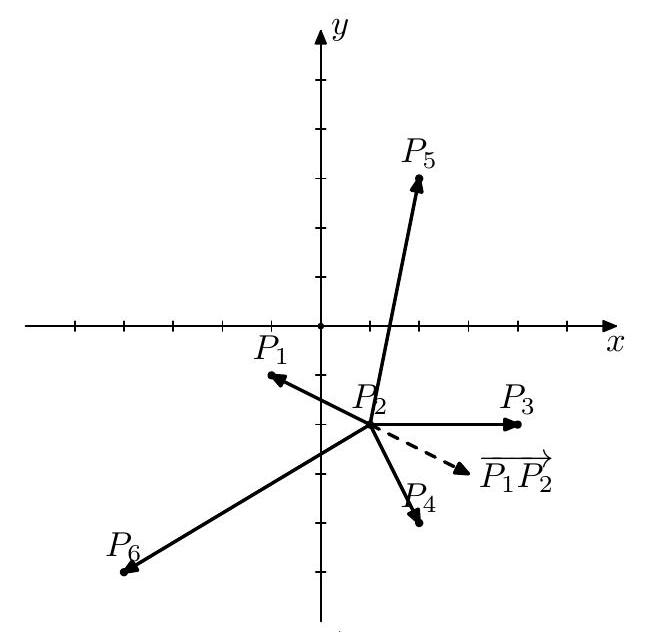
$$\text{图 2:向量} \overrightarrow{P_{1} P_{2}} \text{以及从点} P_{2} \text{到其他所有点的向量}
$$
点将按以下顺序排序:P 3 , P 5 , P 1 , P 6 , P 4 P_{3}, P_{5}, P_{1}, P_{6}, P_{4} P 3 , P 5 , P 1 , P 6 , P 4 6 6 6 2 2 2 6 6 6
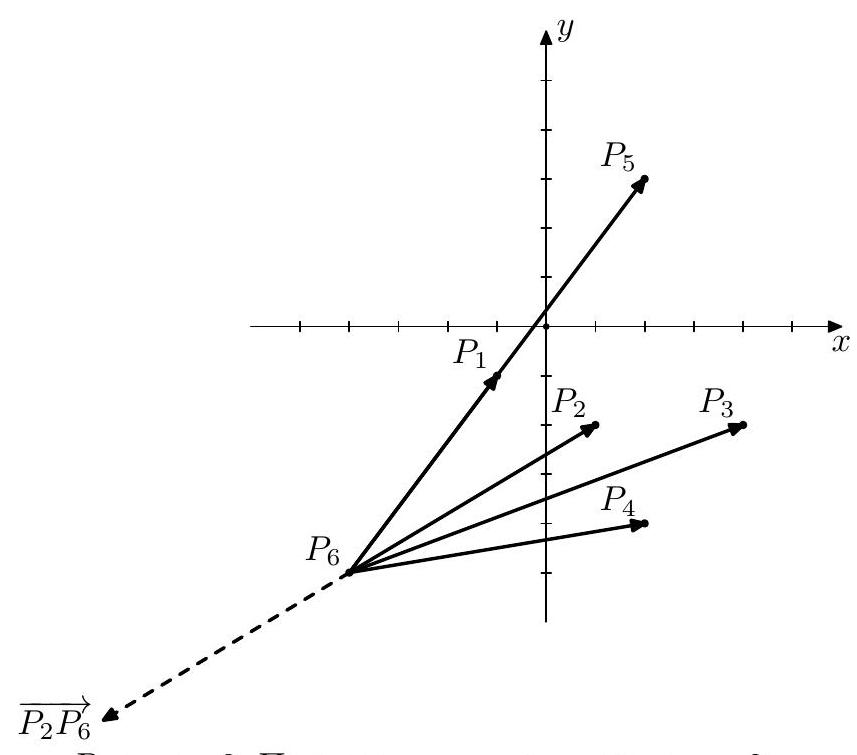
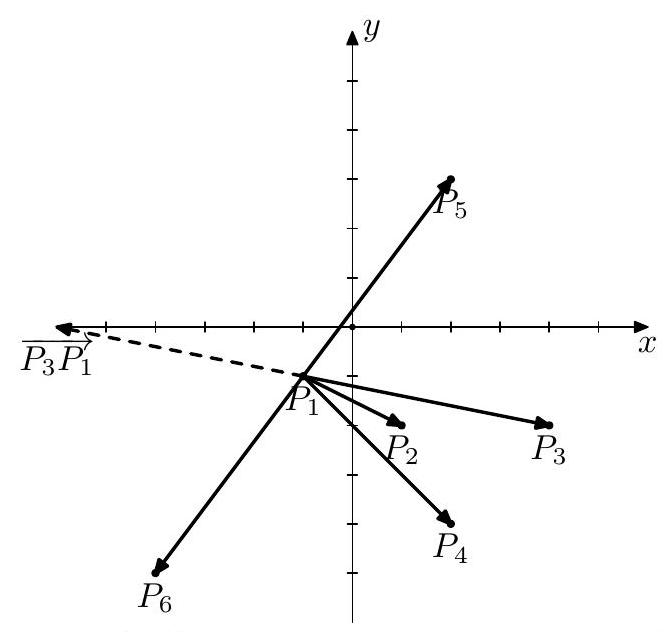
在图 3 中,展示了起始点为 2 2 2 6 6 6 P 4 , P 3 , P 2 , P 1 , P 5 P_{4}, P_{3}, P_{2}, P_{1}, P_{5} P 4 , P 3 , P 2 , P 1 , P 5 P 1 P_{1} P 1 P 5 P_{5} P 5 P 1 P_{1} P 1 P 6 P_{6} P 6 P 5 P_{5} P 5 P 6 P_{6} P 6 1 1 1
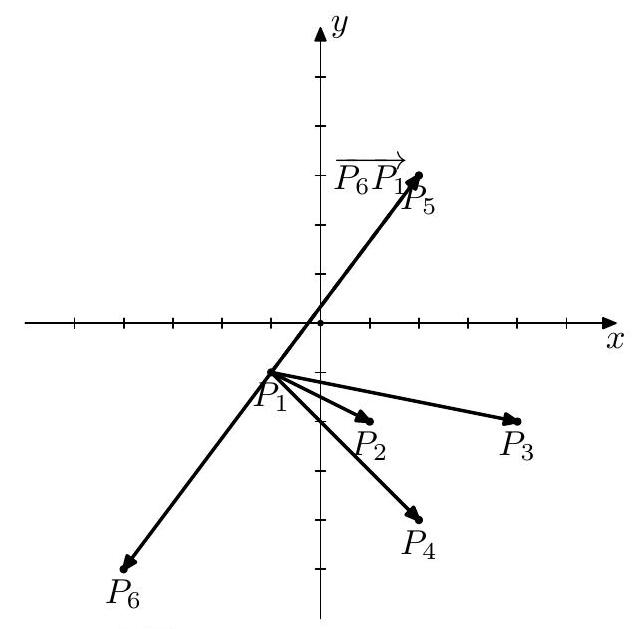
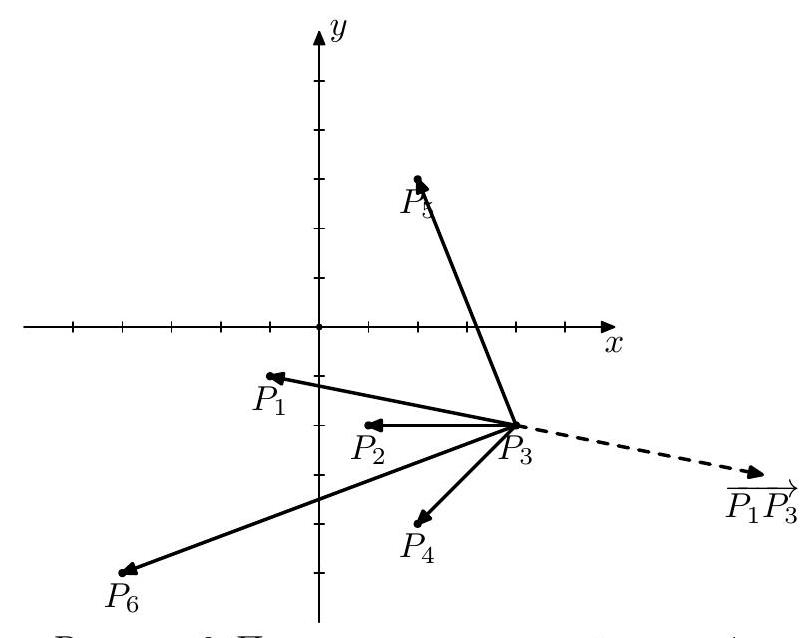
在图 4 中,展示了起始点为 6 6 6 1 1 1 P 1 P_{1} P 1 P 6 P 1 → \overrightarrow{P_{6} P_{1}} P 6 P 1 P 1 P_{1} P 1 P 1 P 5 → \overrightarrow{P_{1} P_{5}} P 1 P 5 P 5 , P 6 , P 4 , P 2 , P 3 P_{5}, P_{6}, P_{4}, P_{2}, P_{3} P 5 , P 6 , P 4 , P 2 , P 3 2 2 2 1 1 1 2 2 2
图 3:起始点为 2,紧随其后的点为 6 的过程
图 4:起始点为 6,紧随其后的点为 1 的过程
我们将每个点涂成三种颜色之一。第 i i i
如果存在一个点 j j j i i i j j j i i i i i i
如果点 i i i j j j i i i j j j i i i i i i
如果点 i i i i i i
确定每个点的颜色。
输入格式
第一行包含两个整数 n n n t t t ( 2 ≤ n ≤ 1000 , 1 ≤ t ≤ n − 1 ) (2 \leq n \leq 1000, 1 \leq t \leq n-1) ( 2 ≤ n ≤ 1000 , 1 ≤ t ≤ n − 1 )
接下来的 n n n x i x_{i} x i y i y_{i} y i ( − 10 9 ≤ x i , y i ≤ 10 9 ) (-10^9 \leq x_{i}, y_{i} \leq 10^9) ( − 1 0 9 ≤ x i , y i ≤ 1 0 9 )
输出格式
输出一个由 n n n i i i i i i G 表示,蓝色点用字母 B 表示,红色点用字母 R 表示。
6 4
-1 -1
1 -2
4 -2
2 -4
2 3
-4 -5
GGBBRG
我们来看第一个样例中的一些点。
点 P 1 P_{1} P 1 P 2 P_{2} P 2 P 1 P_{1} P 1
可以证明,点 P 3 P_{3} P 3 1 1 1 3 3 3 1 1 1 3 3 3
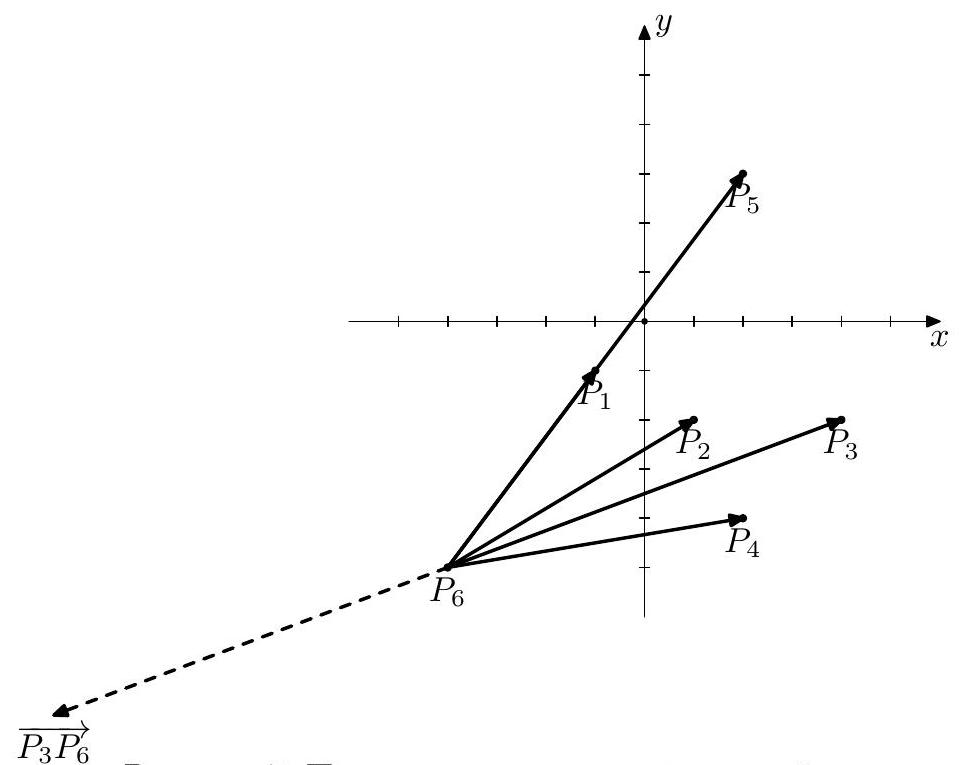
对于起始点 3 3 3 1 1 1 P 6 , P 4 , P 2 , P 3 , P 5 P_{6}, P_{4}, P_{2}, P_{3}, P_{5} P 6 , P 4 , P 2 , P 3 , P 5 3 3 3 1 1 1 3 3 3 P 5 , P 1 , P 2 , P 6 , P 4 P_{5}, P_{1}, P_{2}, P_{6}, P_{4} P 5 , P 1 , P 2 , P 6 , P 4 6 6 6 3 3 3 6 6 6 P 4 , P 3 , P 2 , P 1 , P 5 P_{4}, P_{3}, P_{2}, P_{1}, P_{5} P 4 , P 3 , P 2 , P 1 , P 5 1 1 1
过程继续,起始点为 6 6 6 1 1 1 6 6 6 1 1 1 2 2 2
图 5:起始点为 3,紧随其后的点为 1 的过程
图 6:起始点为 1,紧随其后的点为 3 的过程
图 7:起始点为 3,紧随其后的点为 6 的过程
2 1
1 1
2 2
GG
在第二个样例中,可以很容易地证明,如果一个点是起始点,另一个点是紧随其后的点,那么目标点将是原来的起始点。因此,这两个点都将被涂成绿色。
数据范围与提示
详细子任务附加限制及分值如下表所示。
子任务
分值
附加限制
子任务依赖
1 1 1 10 10 10 n ≤ 10 n \leq 10 n ≤ 10
2 2 2 15 15 15 所有点在一条直线上
1 1 1
3 3 3 10 10 10 n ≤ 10 n \leq 10 n ≤ 10
4 4 4 10 10 10 n ≤ 10 n \leq 10 n ≤ 10 1 , 3 1,3 1 , 3
5 5 5 15 15 15 n ≤ 100 n \leq 100 n ≤ 100 3 3 3
6 6 6 15 15 15 n ≤ 100 n \leq 100 n ≤ 100 1 , 3 , 4 , 5 1,3,4,5 1 , 3 , 4 , 5
7 7 7 5 5 5 n ≥ 3 n \geq 3 n ≥ 3
8 8 8 20 20 20 无附加限制
1 ∼ 7 1\sim 7 1 ∼ 7