#HK4320. 「ROIR 2024 Day1」登机安排
「ROIR 2024 Day1」登机安排
题目描述
译自 ROI Regional 2024 Day1 T1. Посадка в самолет
在比特航空公司的飞机上,座位分布为 排,每排有六个座位,第三个和第四个座位之间有过道。一些乘客提前在线上登记,另一些乘客在机场的登记柜台登记。
在线登记时,乘客可以选择任何座位,并且不能更改。例如,当 时,在线登记后的座位安排可能如下图所示(用叉号表示已占用的座位):
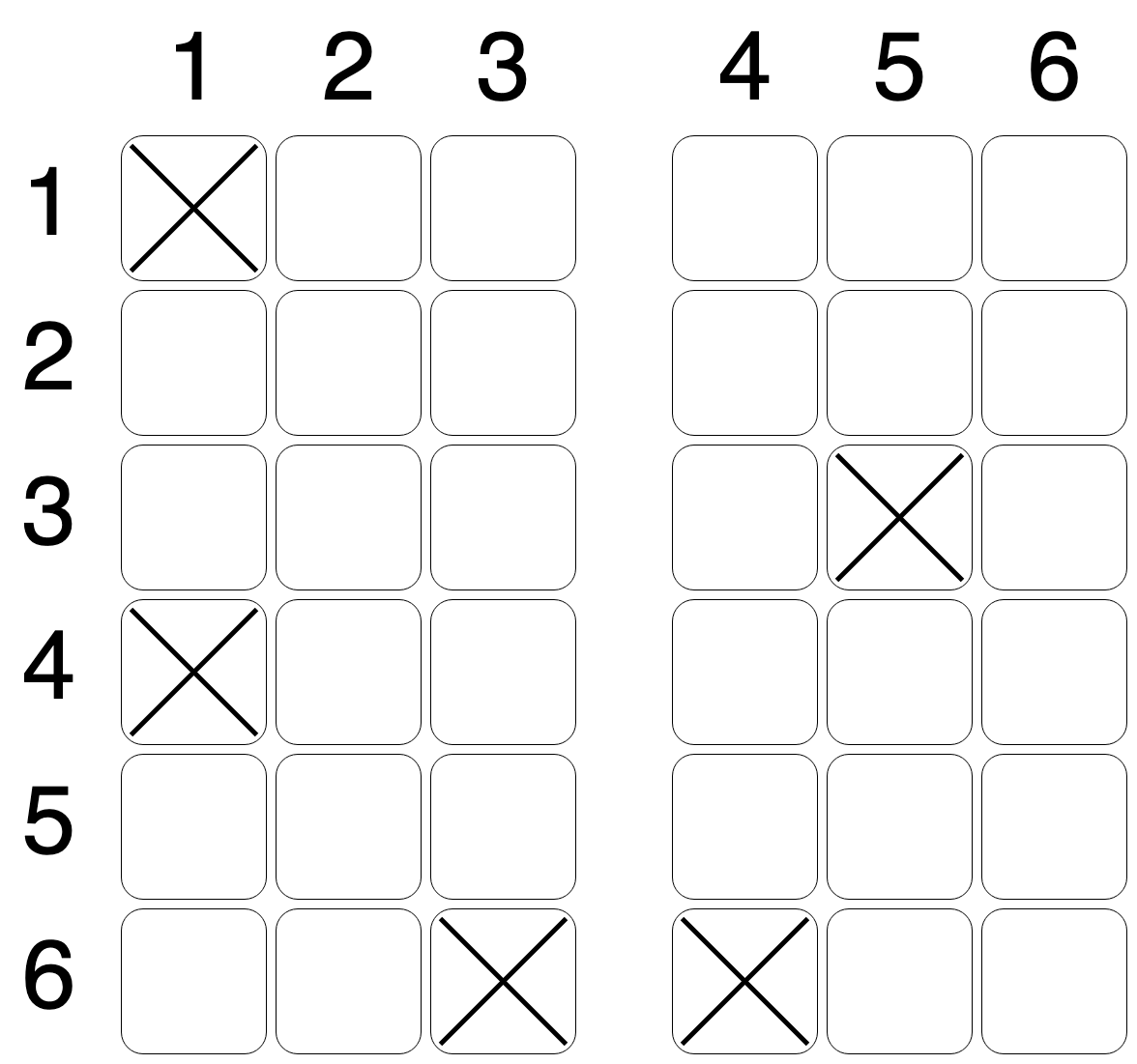
将有 名乘客来到登记柜台。根据比特航空的规定,需要将他们安排在飞机上,使得最终的座位安排相对于过道是对称的。也就是说,如果某排的第一个座位上有乘客,那么同排的第六个座位上也必须有乘客。同样地,第二个和第五个座位,第三个和第四个座位也必须对称。已经在线登记的乘客不能更换座位。在上图所示的初始座位安排中,可以添加七名乘客,使其满足对称条件,例如如下图所示:
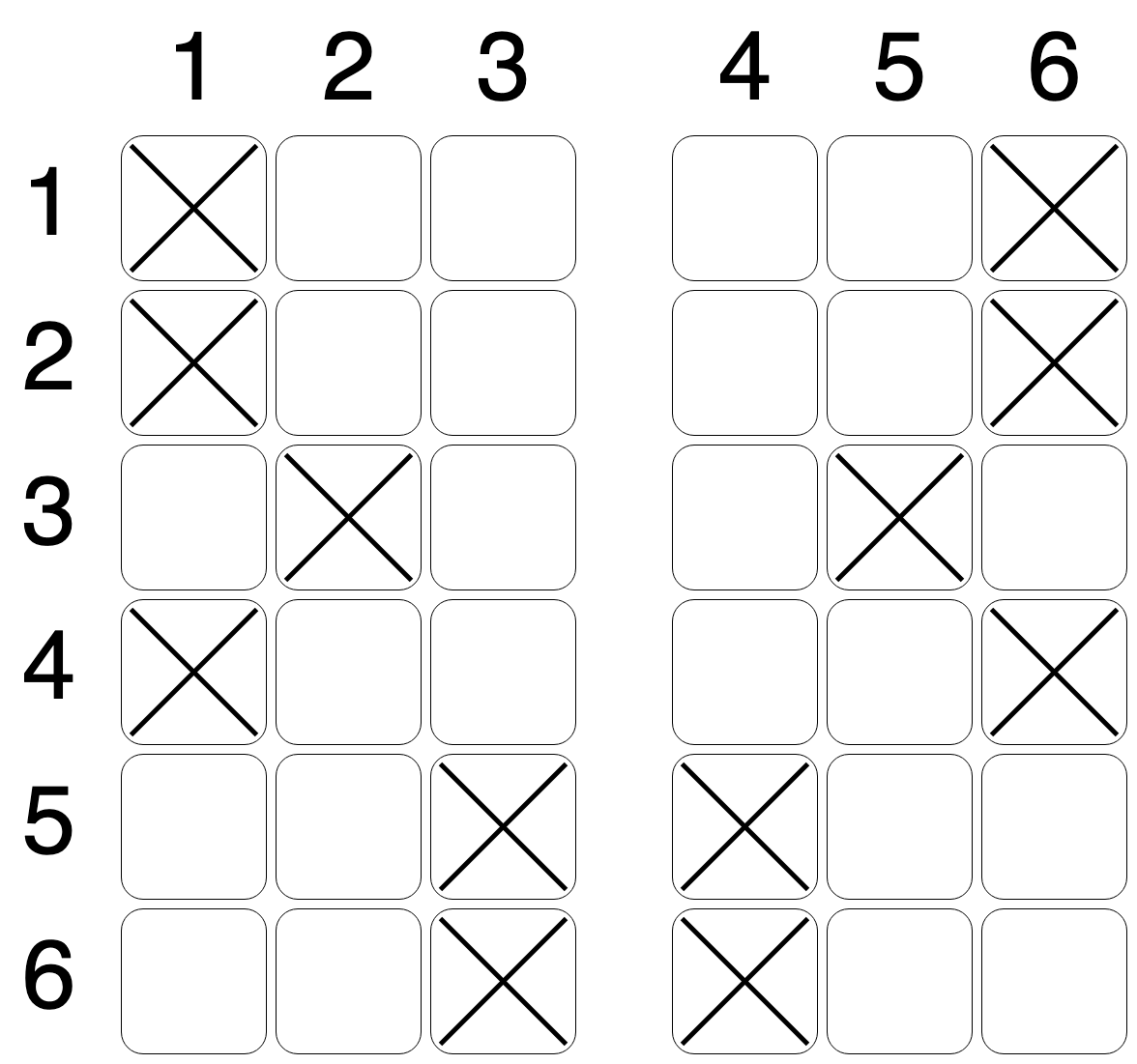
给定在线登记后的座位安排。需要安排 名乘客,使得最终的座位安排相对于过道是对称的,或者确定这是不可能的。
输入格式
第一行包含两个整数 和 ,分别表示飞机的排数和将要登记的乘客数量。
接下来的 行表示在线登记后的初始座位安排。每行包含六个字符,第 行第 个字符为 X,表示第 排第 个座位已被占用;为 .,表示该座位空闲。
输出格式
如果无法找到符合要求的座位安排,输出 Impossible。
否则,输出 行,每行六个字符,表示最终的座位安排。第 行第 个字符为 X,表示座位已被占用;为 .,表示座位空闲。如果存在多个解决方案,可以输出任意一个。
1 0
X.XX.X
X.XX.X
在第一个样例中,,座位安排已经是对称的,因此最终的座位安排与初始安排相同。
2 1
X.XX.X
..X...
X.XX.X
..XX..
在第二个样例中,只有一种方法可以对称地安排乘客。
3 2
X.XX.X
......
X..X.X
Impossible
在第三个样例中,如果 ,存在解决方案,但 时不存在对称安排所有乘客的方法。
1 103
.X.XXX
Impossible
在第四个样例中,需要安排的乘客数量超过了飞机上的空闲座位数量。
6 7
X.....
......
....X.
X.....
......
..XX..
X....X
X....X
.X..X.
X....X
..XX..
..XX..
第五个样例对应于题目描述中的图示情况。在这个样例中存在多个解决方案,给出了其中一种。
数据范围与提示
详细子任务附加限制及分值如下表所示。
| 子任务 | 分值 | 附加限制 | 子任务依赖 |
|---|---|---|---|
| 初始时飞机上所有座位都是空的 | |||
| 初始时飞机上只有一个座位被占用 | |||
| 无附加限制 |