题目描述
题目译自 XXV Olimpiada Informatyczna — I etap Pionek
在一个无限网格的 (0,0) 点上,站着一枚棋子。它有 n 种可用的移动方式,每种方式用一个整数坐标的向量表示。棋子每种移动方式最多使用一次,可以按任意顺序执行。如果向量有重复,棋子可以分别使用每个重复的向量。
你的目标是让棋子尽可能跳到离起点 (0,0) 最远的地方(按欧几里得距离计算)。它能跳多远呢?
输入格式
输入的第一行是一个正整数 n,表示棋子的可用移动次数。
接下来的 n 行,每行包含两个整数 xi,yi (−104≤xi,yi≤104),表示一个移动向量 [xi,yi]。
输出格式
输出一个整数,表示棋子能到达的最远点与 (0,0) 的距离平方。
5
2 -2
-2 -2
0 2
3 1
-3 1
26
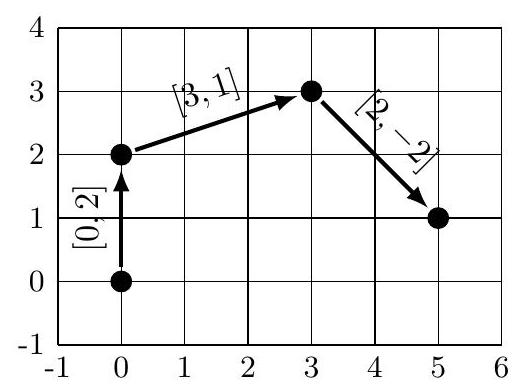
图中展示了一个最优解,使用了向量 [0,2],[3,1],[2,−2]。另一个最优解是用 [0,2],[−3,1],[−2,−2]。
附加样例
- n=5,向量为 [0,0],[1,0],[0,−1],[−1,0],[0,1];
- n=100,向量为 [i,j],其中 i,j∈{1,2,…,10};
- n=200000,所有向量均为 [−1,−1]。
数据范围与提示
详细子任务附加限制及分值如下表所示。
| 子任务 |
附加限制 |
分值 |
| 1 |
n≤20 |
15 |
| 2 |
n≤2000 |
45 |
| 3 |
n≤200000 |
40 |
