题目描述

题目译自 European Girls' Olympiad in Informatics 2023 Day1 T4. Bikes vs Cars

在瑞典的隆德，自行车是非常普遍的交通方式。然而，狭窄的街道上同时容纳汽车和自行车手常常很困难。为了改善这种情况，当地政府决定彻底重新设计街道网络。

隆德有 $N$ 个重要地点（编号从 $0$ 到 $N-1$），人们经常在这些地点之间往返。人们通过路径（即从一个地点到另一个地点的一系列街道）在两地之间旅行。一辆车（汽车或自行车）只有在路径上所有相关车道的宽度不小于车辆宽度时才能通行。每条新建街道连接两个重要地点，总宽度为 $W$，你可以任意分配自行车道和汽车道的宽度。隆德的工程师们最近发明了宽度为 $0$ 的汽车和自行车（这些车辆可以在宽度为 $0$ 的车道上通行）。

工程师们测量了城市中汽车和自行车的宽度。对于每对重要地点，他们知道能在两地间通行的最宽汽车和最宽自行车宽度，但政府还要求不能有更宽的汽车或自行车通过。

形式上，对于每对地点 $i,j$ $(0 \leq i < j \leq N-1$)，你会得到两个整数 $C_{i,j}$ 和 $B_{i,j}$。你的任务是构建一个连接 $N$ 个地点的街道网络。每条街道宽度为 $W$，但你可以为每条街道 $s$ 决定其自行车道宽度 $b_s$，从而汽车道宽度为 $W - b_s$。网络必须满足以下条件：

• 每对地点之间可以通行（可能需要宽度为 $0$ 的自行车或汽车）。
• 对于每对地点 $i,j$ $(i < j)$，存在一条路径，仅使用汽车道宽度至少为 $C_{i,j}$ 的街道，从 $i$ 到 $j$。同时，$C_{i,j}$ 是满足此条件的最大值，即 $i$ 到 $j$ 的所有路径中，至少有一条街道的汽车道宽度不超过 $C_{i,j}$。
• 对于每对地点 $i,j$ $(i < j)$，存在一条路径，仅使用自行车道宽度至少为 $B_{i,j}$ 的街道，从 $i$ 到 $j$。同时，$B_{i,j}$ 是满足此条件的最大值。

你能帮助隆德政府设计这样的街道网络吗？由于资金有限，你最多可以建造 $2023$ 条街道。你可以在同一对重要地点之间建造多条街道，但不能连接同一地点。所有街道均可双向通行。

输入格式

第一行包含两个整数 $N,W$，分别表示隆德的重要地点数量和可建造街道的宽度。

接下来的 $N-1$ 行包含整数 $C_{i,j}$。第 $j$ 行包含所有满足 $i < j$ 的 $C_{i,j}$。因此，第一行仅包含 $C_{0,1}$，第二行包含 $C_{0,2}$ 和 $C_{1,2}$，第三行包含 $C_{0,3}, C_{1,3}, C_{2,3}$，依此类推。

接下来的 $N-1$ 行以相同格式包含整数 $B_{i,j}$。

输出格式

如果无法构建这样的街道网络，输出一行字符串 NO。

否则，第一行输出一个整数 $M$，表示网络中的街道数量。

接下来的 $M$ 行，每行输出三个整数 $u, v, b$，表示在 $u$ 和 $v$ 之间有一条自行车道宽度为 $b$（汽车道宽度为 $W-b$）的街道。

你最多可使用 $2023$ 条街道。输出的街道必须满足 $0 \leq b \leq W$，$0 \leq u, v \leq N-1$ 且 $u \neq v$。你可以在同一对重要地点之间使用多条街道（自行车道宽度可能不同）。

如果存在多种解决方案，你可以输出任意一种。

2 1
1
1

2
0 1 0
0 1 1

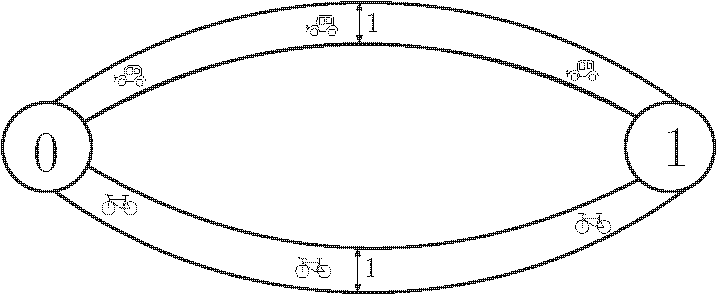
街道宽度为 $1$，地点 $0$ 和 $1$ 之间需要汽车道和自行车道宽度至少为 $1$。解决方案是建造两条连接 $0$ 和 $1$ 的街道，一条自行车道宽度为 $1$（汽车道宽度为 $0$），另一条汽车道宽度为 $1$（自行车道宽度为 $0$）。

4 1
0
0 1
0 0 1
1
1 1
1 1 1

NO

街道宽度为 $1$，每对地点之间需要自行车道宽度为 $1$ 的路径，且地点 $1$ 到 $2$ 和 $2$ 到 $3$ 之间存在汽车道宽度为 $1$ 的路径。由于 $C_{1,3}=0$，从 $1$ 到 $3$ 不应存在汽车道宽度为 $1$ 的路径。然而，连接 $1$ 到 $2$ 和 $2$ 到 $3$ 的路径会形成这样的路径，因此无法构建满足条件的街道网络。

6 6
5
4 4
1 1 1
1 1 1 3
1 1 1 5 3
2
3 2
6 2 3
3 2 5 3
3 2 4 3 4

8
0 1 1
0 2 3
1 2 2
0 3 6
2 4 5
3 4 3
3 5 1
4 5 4

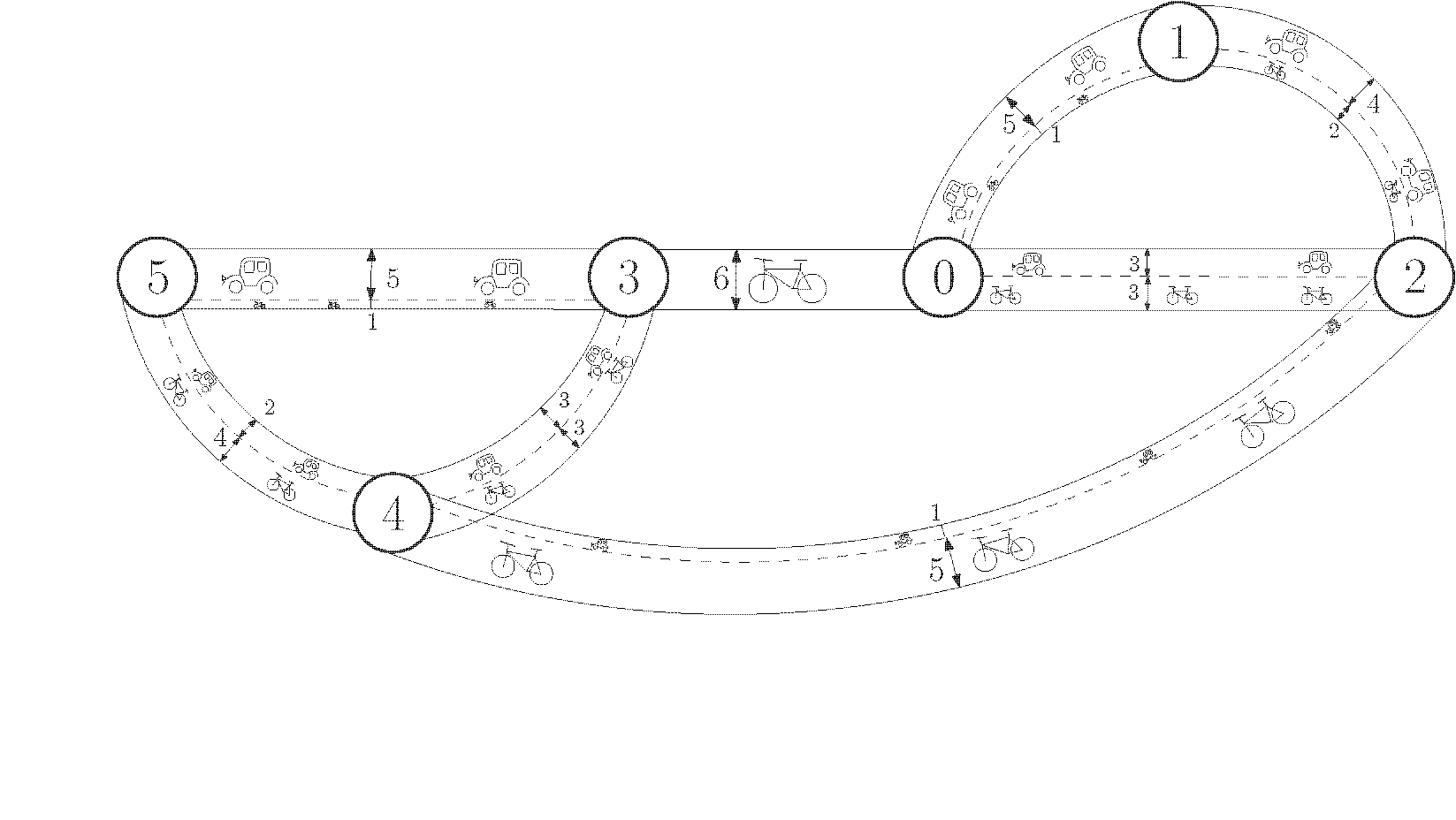
以下街道网络满足所有条件。例如，地点 $0$ 到 $5$ 之间需要汽车道最小宽度为 $1 = C_{0,5}$ 的路径（例如沿 $0 \to 2 \to 4 \to 5$），以及自行车道最小宽度为 $3 = B_{0,5}$ 的路径（例如沿 $0 \to 3 \to 4 \to 5$）。同时，所有连接的路径最小宽度均不超过要求值。注意，样例 3 存在多种其他解决方案。

数据范围与提示

对于所有输入数据，满足：

• $2 \leq N \leq 500$
• $1 \leq W \leq 10^6$
• $0 \leq C_{i,j}, B_{i,j} \leq W$（对于所有 $0 \leq i < j \leq N-1$）

详细子任务附加限制及分值如下表所示。