题目描述

题目译自 European Girls' Olympiad in Informatics 2024 Day1 T1. Infinite Race

在荷兰埃因霍温，每年都会举办一场马拉松。今年，主办方别出心裁，决定让比赛不再止于 42 公里，而是永无止境！为了简化组织，比赛在埃因霍温大学的跑道上进行，参赛者们将在跑道上跑无数圈。

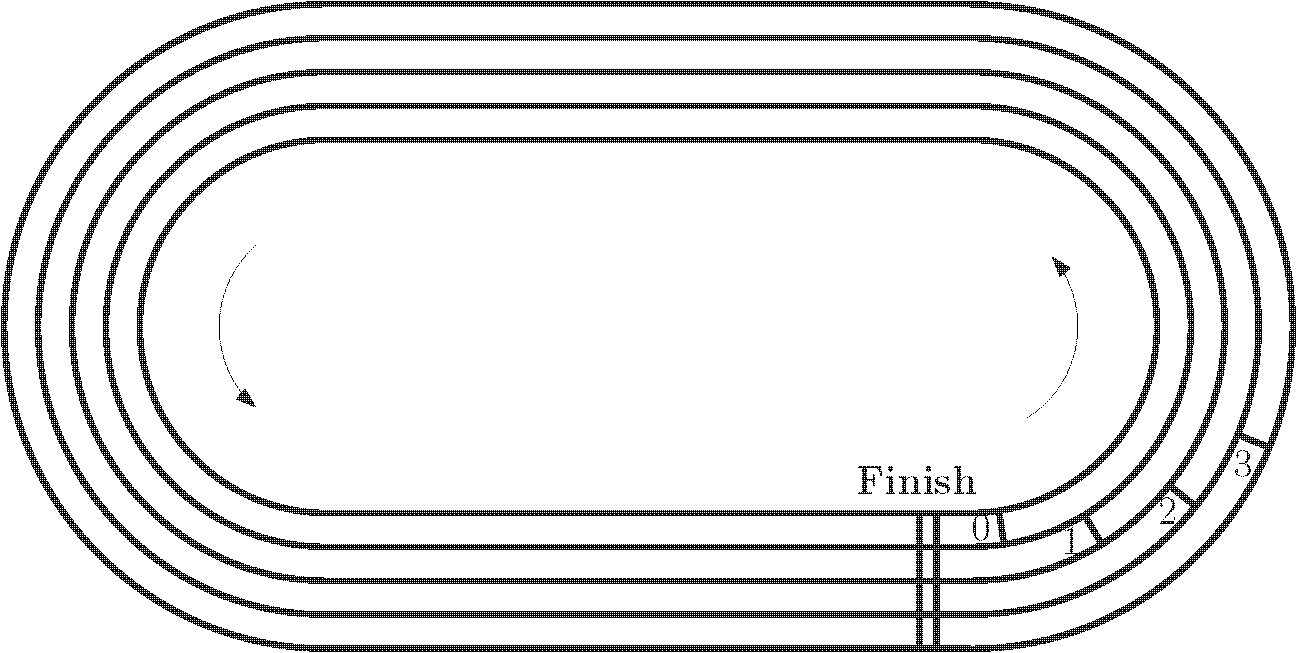
安妮卡兴奋地成为 $N$ 名参赛者之一，编号从 $0$ 到 $N-1$。她报名很快，因此是 $0$ 号选手。比赛开始时，她站在终点线后，其他所有参赛者都在跑道上位于她前方。安妮卡无法记录自己跑了多少圈，但她记得每次超越别人或被别人超越的时刻。你的任务是计算她最少需要穿过终点线多少次。没有人会倒着跑，也不会恰好在终点线上发生超越。此外，参赛者的速度不一定是恒定的。

输入格式

第一行包含一个整数 $N$，表示参赛者数量。

第二行包含一个整数 $Q$，表示事件数量。

接下来的 $Q$ 行按比赛中发生的顺序描述事件。第 $i$ 行包含一个整数 $x_i$：

• 如果 $x_i > 0$，表示安妮卡超越了参赛者 $x_i$。
• 如果 $x_i < 0$，表示参赛者 $-x_i$ 超越了安妮卡。

输出格式

输出一个整数，表示安妮卡最少穿过终点线的次数。

4
5
-2
2
1
-3
2

1

在第一个样例中，有 $N = 4$ 名参赛者和 $Q = 5$ 个事件。你首先被 $2$ 号选手超越，$2$ 号领先你整整一圈。然后，你反超 $2$ 号，接着超越 $1$ 号，再被 $3$ 号超越。此时，你可能仍在第一圈。最后，你再次超越 $2$ 号，这意味着你至少穿过终点线一次。

2
4
1
1
1
1

3

在第二个样例中，除你之外只有一名其他参赛者。你四次超越对方，这意味着你至少穿过终点线三次。

2
5
1
-1
1
-1
-1

0

200000
7
199999
199999
1
199999
55
199999
55

3

3
6
1
2
2
2
1
1

3

数据范围与提示

对于所有输入数据，满足：

• $2 \leq N \leq 200000$
• $1 \leq Q \leq 200000$
• $1 \leq x_i \leq N-1$ 或 $-(N-1) \leq x_i \leq -1$

详细子任务附加限制及分值如下表所示。