题目描述

题目译自 European Girls' Olympiad in Informatics 2024 Day2 T2. Bikeparking

桑娜最近想出了一个赚钱的生意：在埃因霍温火车站出租高端自行车停车位。为了最大化利润，你将停车位分为 $N$ 个不同等级，编号从 $0$ 到 $N-1$。$0$ 号等级是高端等级，位置离火车站台非常近。编号越高的等级，停车位的条件越差。第 $t$ 等级有 $x_t$ 个停车位。

用户通过一个应用分配停车位。每位用户有自己的订阅等级，并期望获得对应等级的停车位。然而，服务条款并不保证用户一定得到其订阅等级的停车位。

如果订阅等级为 $s$ 的用户被分配到等级 $t$ 的停车位，会发生以下三种情况之一：

1. 如果 $t < s$，用户会很开心，给应用点赞。
2. 如果 $t = s$，用户感到满意，不会采取任何行动。
3. 如果 $t > s$，用户会生气，给应用差评。

今天，桑娜的应用有 $y_0 + y_1 + \ldots + y_{N-1}$ 名用户，其中 $y_s$ 是订阅等级 $s$ 的用户数量。你需要帮助桑娜将用户分配到停车位。每个用户必须恰好分配到一个停车位，每个停车位最多分配给一个用户，但允许某些停车位空置。此外，总用户数不超过总停车位数。

桑娜希望最大化应用的评分。设 $U$ 为点赞数，$D$ 为差评数。你的任务是最大化 $U - D$。

输入格式

第一行包含一个整数 $N$，表示停车位等级数或订阅等级数。

第二行包含 $N$ 个整数 $x_0, x_1, \ldots, x_{N-1}$，表示各等级的停车位数量。

第三行包含 $N$ 个整数 $y_0, y_1, \ldots, y_{N-1}$，表示各订阅等级的用户数量。

输出格式

输出一个整数，表示通过最优分配用户到停车位可获得的最大 $U - D$ 值。

2
3 3
1 3

2

在第一个样例中，你可以将订阅等级 $0$ 的用户分配到 $0$ 号等级的停车位，将两名等级 $1$ 的用户分配到 $0$ 号等级的停车位（获得 $2$ 个点赞），将剩余一名等级 $1$ 的用户分配到 $1$ 号等级的停车位。这导致评分 $2$。

3
1 1 1
1 1 1

1

在第二个样例中，你可以将等级 $1$ 的用户分配到 $0$ 号等级的停车位，等级 $2$ 的用户分配到 $1$ 号等级的停车位，等级 $0$ 的用户分配到 $2$ 号等级的停车位。这获得 $2$ 个点赞和 $1$ 个差评，评分 $1$。

6
1 0 1 1 0 1
1 1 0 0 1 0

1

在第三个样例中，你可以将等级 $1$ 的用户分配到 $0$ 号等级的停车位，等级 $0$ 的用户分配到 $2$ 号等级的停车位，等级 $4$ 的用户分配到 $3$ 号等级的停车位。这同样获得 $2$ 个点赞和 $1$ 个差评，评分 $1$。

4
2 1 1 8
0 4 4 0

-1

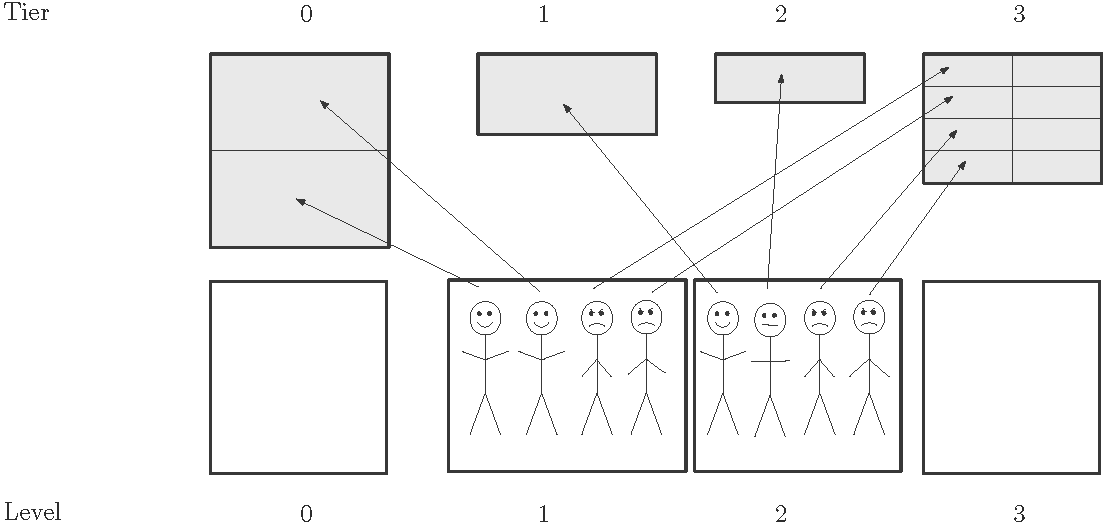
第四个样例如下图所示。你可以将等级 $1$ 的用户分配到 $0, 0, 3, 3$ 号等级的停车位，获得 $2$ 个点赞和 $2$ 个差评；将等级 $2$ 的用户分配到 $1, 2, 3, 3$ 号等级的停车位，获得 $1$ 个点赞和 $2$ 个差评。共 $3$ 个点赞和 $4$ 个差评，评分 $-1$。

1
1000000000
1000000000

0

在第五个样例中，你可以将所有用户分配到与他们订阅等级匹配的停车位，评分 $0$。

数据范围与提示

对于所有输入数据，满足：

• $1 \leq N \leq 3 \cdot 10^5$
• $0 \leq x_i, y_i \leq 10^9$（对于 $i = 0, 1, \ldots, N-1$）
• $y_0 + y_1 + \ldots + y_{N-1} \leq x_0 + x_1 + \ldots + x_{N-1} \leq 10^9$

详细子任务附加限制及分值如下表所示。