题目描述

题目译自 XXXII Olimpiada Informatyczna – II etap Drzewo genealogiczne

Bajtazar 最近迷上了追溯自己姓氏的起源。在他的家族中，有个独特的传统：父母姓氏为 $u$ 和 $w$ 的孩子，姓氏为 $u w$ 或 $w u$，由父母自由选择。

Bajtazar 翻遍旧箱子，找到 $n$ 代前的祖先记录，称这些为原始祖先。令人惊讶的是，当时的姓氏仅为单个小写英文字母。$n$ 代前有 $2^n$ 位祖先，因为每人有两个父母、四个祖父母、八个曾祖父母，以此类推。这些祖先编号为 $1$ 到 $2^n$，其中 $1$ 与 $2$ 配对，$3$ 与 $4$ 配对，每对生一个孩子，孩子编号为 $1$ 到 $2^{n-1}$（如 $1$ 和 $2$ 的孩子为 $1$）。此过程逐代重复，直到 Bajtazar 这一代，仅剩他一人。

Bajtazar 的姓氏长度为 $2^n$，但他不清楚其形成过程，因为祖先可自由选择孩子姓氏的字母顺序。他开始怀疑档案记录可能有误，请你帮忙验证。

情况是动态变化的，Bajtazar 会修改档案或自己的姓氏。你的任务是判断初始状态及每次 $q$ 次事件后，他的姓氏是否可能由档案中的祖先姓氏按规则生成。事件 $i$ 为以下两种之一：

1. Bajtazar 将自己姓氏的第 $k_i$ 位字母改为 $b_i$。
2. 原始祖先 $k_i$ 的姓氏改为 $b_i$（$b_i$ 为小写字母）。

输入格式

第一行包含两个整数 $n, q$ $(1 \leq n \leq 20, 0 \leq q \leq 1000000)$，表示代数和事件数。

第二行包含 $2^n$ 个小写英文字母，描述 Bajtazar 的姓氏。

第三行包含 $2^n$ 个小写英文字母，第 $i$ 个字母表示原始祖先 $i$ 的姓氏。

接下来的 $q$ 行描述事件，第 $i$ 行包含两个整数 $t_i, k_i$ 和一个小写字母 $b_i$ $(1 \leq t_i \leq 2, 1 \leq k_i \leq 2^n)$。若 $t_i=1$，表示修改 Bajtazar 姓氏第 $k_i$ 位为 $b_i$；若 $t_i=2$，表示修改祖先 $k_i$ 的姓氏为 $b_i$。

输出格式

输出 $q+1$ 行。第一行表示初始状态的答案，接下来的 $q$ 行按事件顺序表示每次事件后的答案。若 Bajtazar 的当前姓氏可由档案姓氏按规则生成输出 TAK，否则输出 NIE。

2 4
abcd
cadb
1 2 c
2 4 c
1 1 d
1 4 a

NIE
NIE
TAK
NIE
TAK

初始及每次事件后的情况如下：

1. Bajtazar 姓氏为 abcd，祖先姓氏为 c, a, d, b。不可生成，答案为 NIE。

2. Bajtazar 姓氏为 accd，祖先姓氏不变。不可生成，答案为 NIE。

3. Bajtazar 姓氏为 accd，祖先姓氏为 c, a, d, c。可生成，父母姓氏为 ac 和 cd，答案为 TAK。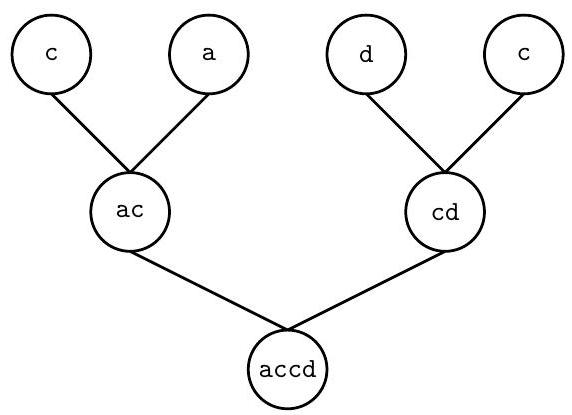

4. Bajtazar 姓氏为 dccd，祖先姓氏不变。不可生成，答案为 NIE。

5. Bajtazar 姓氏为 dcca，祖先姓氏不变。可生成，父母姓氏为 ca 和 dc，答案为 TAK。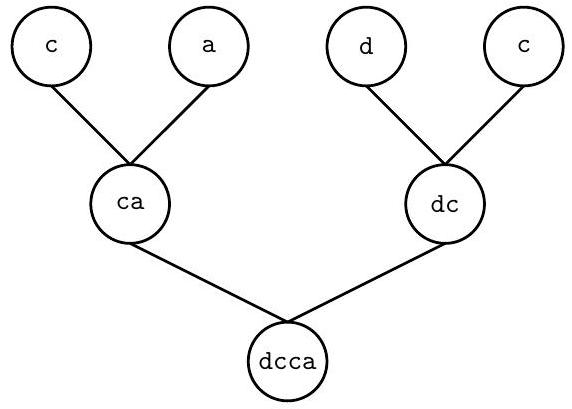

附加样例

1. $n=3, q=10$，测试仅含字母 a 和 b。
2. $n=10, q=1000$，初始 Bajtazar 姓氏为祖先姓氏的镜像，保持每两事件后此性质。
3. $n=20, q=0$，Bajtazar 姓氏全为 a，祖先姓氏全为 b，答案为 NIE。
4. $n=18, q=200000$，初始两字符串全为 a，每两事件将对应位置改为 b。
5. $n=20, q=1000000$，Bajtazar 姓氏由 xyzw 多次重复，祖先姓氏由 yxzw 重复，事件将前者改为 zyxw 重复，后者改为 yzxw 重复，每四事件答案为 TAK，其余为 NIE。

数据范围与提示

详细子任务附加限制及分值如下表所示。