题目描述
题目译自 XXXII Olimpiada Informatyczna – III etap Lokacja miasta
Bajtazar 终于为新城 Bajtowo 找到了理想的建设地点。他尚未确定城市的最终规模,但已规划了一个直角坐标系,决定城市将是一个与坐标轴平行的矩形区域,左下角固定在点 (0,0),右上角位于待定的点 (W,H),其中 W,H 为正整数。
为规划城市布局,Bajtazar 决定划定 n+1 条平行大道,编号从 0 到 n,第 i 条大道连接点 (xi,0) 和 (xi,H)。同时,他将划定 m+1 条平行街道,编号从 0 到 m,第 j 条街道连接点 (0,yj) 和 (W,yj)。由于技术要求,所有待定坐标 xi 和 yj 必须是整数,且满足 0=x0<x1<…<xn=W 以及 0=y0<y1<…<ym=H。这些大道和街道将城市分割成 n⋅m 个矩形地块,位于第 i−1 和 i 条大道、第 j−1 和 j 条街道之间的地块记为 (i,j)。
Bajtazar 与 l 位未来居民保持联系,收集了他们的地块偏好。第 k 位居民希望居住在地块 (ak,bk),并要求该地块面积恰为 pk 平方米(1≤pk≤r,r 为输入参数)。保证任意两位居民的偏好地块不同,即对于 i=j,(ai,bi)=(aj,bj)。未被居民选中的地块面积可任意。你的任务是判断能否满足所有居民的面积要求,若能,计算满足要求的最小城市总面积。
输入格式
第一行包含四个整数 n,m,l,r $(1 \leq n, m \leq 10^3, 1 \leq l \leq n \cdot m, 1 \leq r \leq 10^6)$,分别表示大道数、街道数、居民数和面积上限。
接下来的 l 行,每行包含三个整数 ai,bi,pi $(1 \leq a_i \leq n, 1 \leq b_i \leq m, 1 \leq p_i \leq r)$,表示第 i 位居民希望居住在地块 (ai,bi),要求面积为 pi。
输出格式
第一行输出 TAK 或 NIE,表示是否能满足所有居民的面积要求。
若为 TAK,第二行输出一个整数 p,表示满足所有要求的最小城市总面积。
2 2 3 100
1 1 7
1 2 13
2 1 1
NIE
2 2 3 100
1 1 7
1 2 14
2 1 1
TAK
24
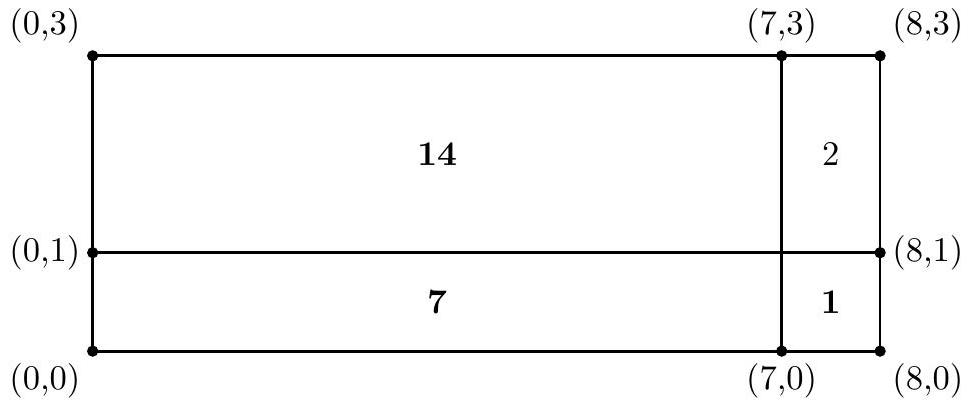
在样例 2 中,可设置 x0=0,x1=7,x2=8 和 y0=0,y1=1,y2=3。地块 (1,1) 面积为 (x1−x0)(y1−y0)=7⋅1=7,(1,2) 面积为 (x1−x0)(y2−y1)=7⋅2=14,(2,1) 面积为 (x2−x1)(y1−y0)=1⋅1=1,满足居民要求。城市总面积为 W⋅H=x2⋅y2=8⋅3=24。
附加样例
- n=m=10,l=r=100,$a_i = ((i-1) \bmod 10) + 1, b_i = \lfloor (i-1)/10 \rfloor + 1, p_i = i$,答案为
NIE。
- n=m=l=r=100,ai=bi=pi=i,答案为
TAK,505000。
- n=m=1000,l=r=10,答案为
TAK,174749957037。
数据范围与提示
详细子任务附加限制及分值如下表所示。
| 子任务编号 |
附加限制 |
分值 |
| 1 |
n=1 |
9 |
| 2 |
n,m≤6,r≤100 |
11 |
| 3 |
n,m≤100,r≤1000 |
16 |
| 4 |
r≤1000 |
19 |
| 5 |
l=n⋅m |
21 |
| 6 |
无附加限制 |
24 |
若仅第一行正确,程序可获 50% 的分数。
