题目描述
题目译自 XXXI Olimpiada Informatyczna – II etap Rycerz
在 Bajtocja 王国,有 n 座城市通过 m 条双向道路相连,每条道路通行需耗时一天。城市编号从 1 到 n。一位骑士从城市 1 出发,需在最多 d 天内抵达城市 n,挑战一只强大的怪兽。
骑士将使用 k 把不同类型的剑,类型编号从 1 到 k,每把剑具有非负整数值。初始时,骑士持有每种类型的剑,价值均为 0。每条道路旁驻扎 k 名剑匠,第 i 条道路的第 j 名剑匠可将类型 j 的剑价值调整为 ai,j。骑士通过道路时,可选择任意剑匠调整任意子集的剑,每种剑可多次调整。
骑士希望最大化类型 1 的剑价值;在保证类型 1 价值最大的前提下,最大化类型 2 的剑价值,依此类推,直至类型 k。调整顺序无关紧要,仅关注最终价值。已知道路网络保证从城市 1 到 n 在 d 天内可达,骑士可多次经过城市或道路。你的任务是确定骑士在最佳路径规划下的剑价值。
输入格式
第一行包含四个整数 n,m,d,k $(2 \leq n \leq 10000, 1 \leq m, d \leq 10000, 1 \leq k \leq 10)$,分别表示城市数、道路数、最多天数和剑类型数。
接下来的 m 行,每行包含 k+2 个整数 ui,vi,ai,1,…,ai,k,描述第 i 条道路。其中 ui,vi (1≤ui,vi≤n,ui=vi) 表示道路连接的城市编号,ai,j (0≤ai,j≤109) 表示第 j 名剑匠可将类型 j 的剑调整为该价值。同一城市对可能有多条道路。
输出格式
输出一行,包含 k 个非负整数 w1,…,wk,以空格分隔。w1 表示骑士在最多 d 天内抵达城市 n 可获得的最大类型 1 剑价值;w2 表示在 w1 最大前提下,类型 2 剑的最大价值,依此类推。即,序列 (w1,…,wk) 是骑士在 d 天内抵达 n,各类型 j 剑达 wj 价值的最大字典序序列。
7 7 6 2
1 2 7 9
2 7 1 0
1 3 5 6
3 4 10 1
4 7 0 0
5 6 2 17
5 7 3 15
10 15
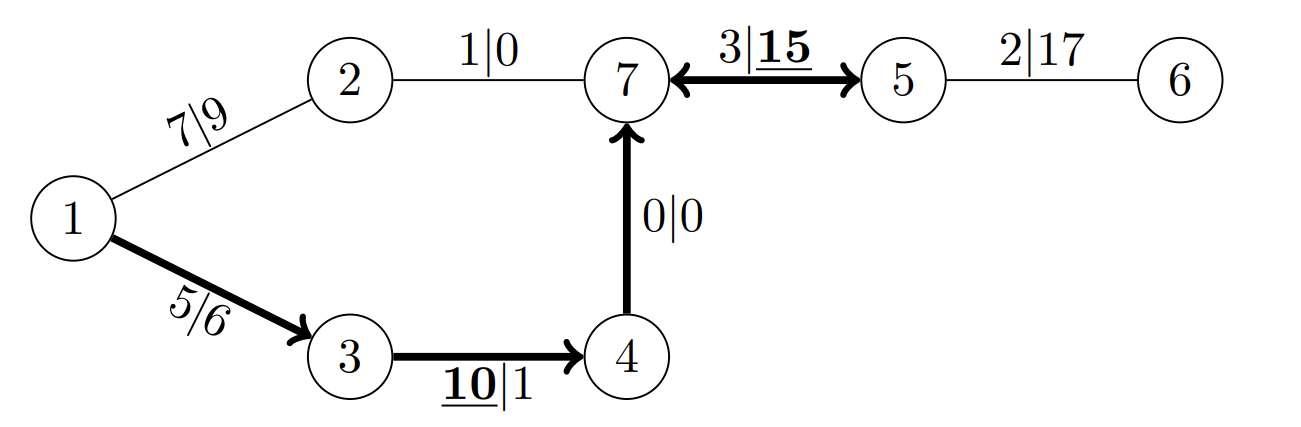
最佳路径在图示中以粗线和箭头标示,按骑士通行方向绘制,粗体下划线标签表示道路上执行的剑调整。
从城市 3 到 4 的道路提供类型 1 剑的最大价值 10。无法在 6 天内同时经过 3 到 4 和 5 到 6 的道路。因此,骑士选择类型 2 剑价值 15,通过 5 到 7 的道路。路径为 1,3,4,7,5,7,剩余 1 天未使用。
附加样例
- n=5,m=4,d=3,k=4,每座城市与城市 1 相连,每条道路仅一个剑匠可将剑调整为非 0 价值。
- n=100,m=4950,d=5,k=8,每座城市与所有其他城市相连,剑价值随机。
- n=10000,m=9999,d=n−1,k=1,城市 i 与 i+1 (1≤i≤n−1) 相连。
数据范围与提示
详细子任务附加限制及分值如下表所示。
| 子任务编号 |
附加限制 |
分值 |
| 1 |
n,m,d≤10 |
10 |
| 2 |
k=1 |
15 |
| 3 |
n,m,d≤500,k≤5 |
15 |
| 4 |
n,m,d≤1000,ai,j≤10 |
20 |
| 5 |
n,m,d≤1000 |
15 |
| 6 |
无附加限制 |
25 |
