题目描述

题目译自 XX Olimpiada Informatyczna — II etap Łuk triumfalny

Bajtocja 的国王 Bajtazar 凯旋归国。Bajtocja 有 $n$ 座城市，仅由 $n-1$ 条道路连接，任意两城之间存在唯一路径（即道路网络构成一棵树）。

国王刚进入首都，编号为 $1$ 的城市，那里已建好一座凯旋门，供他胜利归来时通过。受到臣民热烈欢迎的 Bajtazar 决定举办一场盛大的巡游，计划从首都出发，游历所有城市。

除首都外，其他城市尚未准备迎接国王，未建凯旋门。Bajtazar 的顾问负责监督凯旋门建设，计划雇佣若干建筑队。每队每天可在一座任意城市建造一座凯旋门。遗憾的是，国王的巡游路线未知，仅知他每天从当前城市移动到相邻城市，且可能多次访问同一城市（但每城只需一座凯旋门）。

顾问需为每队支付相同费用，无论其建造多少凯旋门。他希望确保国王每到一城时，该城已有凯旋门，同时尽量减少雇佣的建筑队数量。请帮助他编写程序，计算所需的最少建筑队数量。

输入格式

第一行包含一个整数 $n$ $(1 \leq n \leq 300000)$，表示 Bajtocja 的城市数量。城市编号从 $1$ 到 $n$，首都为 $1$。

接下来的 $n-1$ 行，每行包含两个整数 $a, b$ $(1 \leq a, b \leq n)$，表示城市 $a$ 和 $b$ 间存在一条双向道路。

输出格式

输出一个整数，表示顾问所需雇佣的最少建筑队数量。

7
1 2
1 3
2 5
2 6
7 2
4 1

3

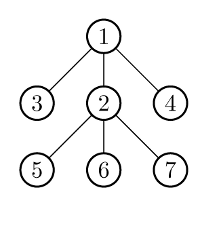
在第一天，需在城市 $2, 3, 4$ 建造凯旋门。之后，在城市 $5, 6, 7$ 建造即可。

附加样例

1. $n=8191$，城市构成高度为 $12$ 的满二叉树。
2. $n=300000$，城市 $1, \ldots, n$ 沿单路径排列。
3. $n=5$，简单正确性样例。
4. $n=6$，简单正确性样例。
5. $n=10000$，九条长路径从根节点垂下。

数据范围与提示

对于 $50\%$ 的数据，$n \leq 10000$。