题目描述

题目译自 XXX Olimpiada Informatyczna – III etap Laptopy

Bajtogrod 学校的所有学生都使用相同的笔记本电脑。教室里摆放着几张相同的课桌，依次排开（每张课桌离黑板稍远一些）。课间前，$n$ 名学生进入教室，各自在课桌旁坐下，打开了笔记本电脑。课间后，又有 $m$ 名学生来到教室。

老师希望每位学生都能坐在课桌旁并打开笔记本电脑。同一课桌可容纳多名学生，但笔记本电脑不能前后重叠（否则会遮挡屏幕），也不能堆叠。为避免掉落，笔记本电脑不得超出课桌边缘，且其边必须与课桌边缘平行（不能斜放）。

形式上，课桌在平面坐标系中表示为尺寸 $w \times s$ 的矩形（$w$ 为平行于黑板的边长），笔记本电脑为无边框的 $d \times s$ 矩形（$s < d \leq w$）。每个笔记本电脑矩形必须完全位于某课桌矩形内，且任意两个笔记本电脑矩形不得有公共点。

请计算最少需要移动（换到其他课桌或在同课桌内挪动位置）多少名初始的 $n$ 名学生，才能让 $n+m$ 名学生及其笔记本电脑都适应课桌？移动一名学生及其笔记本电脑算作一次操作，无论移动距离远近。

考虑多个独立查询（$m$ 的值可能不同）。若某查询无法让所有学生适应课桌，输出 $-1$。

输入格式

第一行包含五个正整数 $n, q, d, l, w$ $(1 \leq q \leq n \leq 3000, 1 \leq l \leq 3000, 1 \leq d, w \cdot l \leq 10^{18})$，分别表示课间前已入座的学生数、查询数、笔记本电脑长度、课桌数和每张课桌的长度。课桌编号为 $1$ 至 $l$，入座学生编号为 $1$ 至 $n$。

接下来的 $n$ 行，每行包含两个整数 $k_i, p_i$ $(1 \leq k_i \leq l, 0 \leq p_i \leq w - d, i=1, \ldots, n)$，表示第 $i$ 名学生坐在第 $k_i$ 号课桌，笔记本电脑左边缘距课桌左边缘的距离为 $p_i$。保证初始的学生和笔记本电脑位置满足题目条件。

下一行包含 $q$ 个整数 $m_1, \ldots, m_q$ $(1 \leq m_i \leq 10^{18})$，描述程序的查询。第 $i$ 个查询表示在 $n$ 名学生按上述位置入座后，新增 $m_i$ 名学生进入教室。每个查询独立。

输出格式

输出 $q$ 行，第 $i$ 行包含一个整数，作为第 $i$ 个查询的答案。若无论学生如何移动，都无法让所有学生适应课桌，输出 $-1$。否则，输出最少需要移动的学生数，以容纳 $n+m_i$ 名学生及其笔记本电脑。

尽管初始位置 $p_i$ 为整数，学生可移动到非整数位置。

4 3 3 2 10
2 1
1 2
1 6
2 5
2 1 3

2
1
-1

对于第一个查询：只需将第二名学生移到第一课桌左端，第四名学生移到第二课桌右端，如图所示。

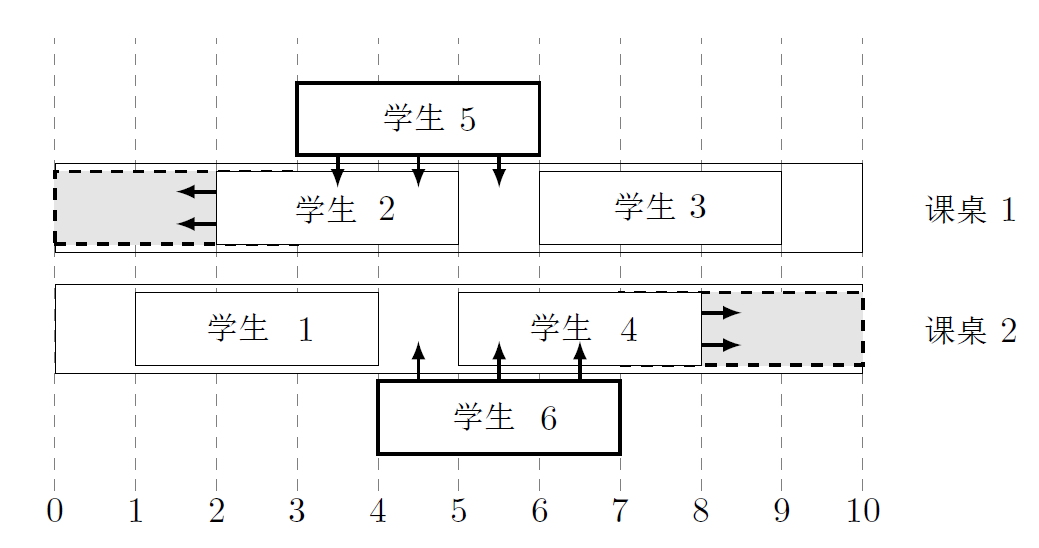
附加样例

1. $n=1, l=1, d=2, w=100, p_1=1$，$q=1, m_1=49$，答案为 $1$。
2. $n=500, l=1, d=7, w=4002, p_i=1+8 \cdot (i-1)$，$q=50, m_i=51-i$，答案为 $299, 293, 287, \ldots, 11, 5$。
3. $n=3000, l=2, d=10^9, w=5 \cdot 10^{12}$，学生在第一课桌从左端开始，间隔 $0, 1, 2, \ldots$，$q=1, m_1=7000$，答案为 $2998$。

数据范围与提示

详细子任务附加限制及分值如下表所示。