题目描述

题目译自 XXX Olimpiada Informatyczna – III etap Tort

今天是 Bajtazar 的生日，$k$ 位宾客齐聚生日派对。Bajtazar 早有准备，烤了一块巨大的蛋糕。现在，他需要将蛋糕切分给每位宾客和自己享用！

Bajtazar 有一张边长 $10^6$ 拜托米的正方形桌子，上面标有坐标系。桌子左下角为 $(0, 0)$，右上角为 $(10^6, 10^6)$。他将蛋糕放在桌上，蛋糕是一个顶点坐标为整数的正交多边形，其每条边平行于桌子的某条边。

Bajtazar 将进行 $k$ 次切割，将蛋糕分成 $k+1$ 份（不一定连通）面积相等的部分。他采用了一种炫酷的切割方式：在桌子左下角 $(0, 0)$ 安装了一台强力激光器。初始时，激光器关闭，指向 $(1, 0)$。随后，他将逆时针缓慢旋转激光器，激光器上的显示屏始终显示其指向的点，该点距左下角恰好 $1$ 拜托米。因此，初始指向 $(1, 0)$，旋转 $45$ 度后指向 $\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)$，再旋转 $45$ 度指向 $(0, 1)$。

在旋转过程中，Bajtazar 将 $k$ 次短暂开启激光器。每次开启，激光沿通过左下角和显示屏指向点的直线，瞬间切割蛋糕。每次切割后，一份（可能不连通）的蛋糕被分离，由下一位宾客取走。经过 $k$ 次切割，剩余的第 $k+1$ 份由 Bajtazar 享用。

然而，Bajtazar 面临难题：何时开启激光，才能确保每位宾客（包括他自己）得到等量的蛋糕？请帮助他确定每次切割时激光器显示屏的指向坐标。

输入格式

第一行包含两个整数 $n, k$ $(4 \leq n \leq 300000, n$ 为偶数 $,1 \leq k \leq 300000)$，分别表示蛋糕的多边形边数和宾客人数。蛋糕顶点按沿边界顺序编号为 $1$ 至 $n$。

接下来的 $n$ 行描述蛋糕，第 $i$ 行包含两个整数 $x_i, y_i$ $(1 \leq x_i, y_i \leq 10^6)$，表示第 $i$ 个顶点的坐标。

保证蛋糕的每条边平行于坐标轴，且相邻两条边垂直。多边形为正交多边形（无重复顶点，仅相邻边在顶点处相交）。

输出格式

输出 $k$ 行，第 $i$ 行包含两个实数 $p_i, q_i$，表示第 $i$ 次切割时激光器指向的点 $(p_i, q_i)$。答案若与正确坐标的差值均不超过 $10^{-6}$，则视为正确。输出数字需保留 $1$ 至 $20$ 位小数，不允许使用科学计数法。

建议：在 C++ 中使用 long double 表示结果。

6 3
2 2
9 2
9 4
4 4
4 9
2 9

0.894427190999916 0.447213595499958
0.707106781186548 0.707106781186548
0.447213595499958 0.894427190999916

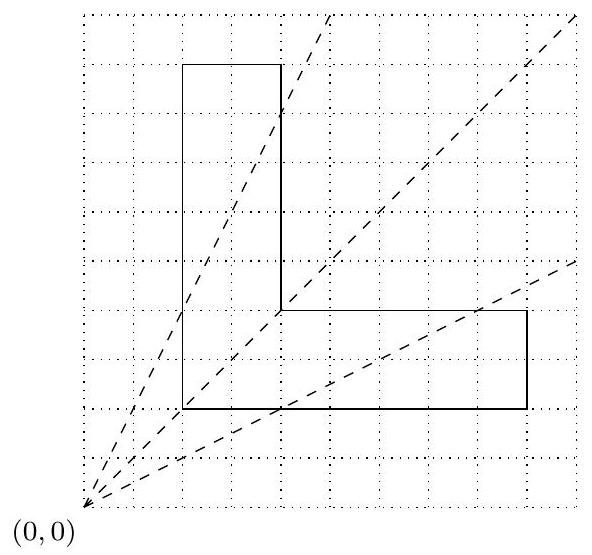
目标坐标为 $\left(\frac{2 \sqrt{5}}{5}, \frac{\sqrt{5}}{5}\right), \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right), \left(\frac{\sqrt{5}}{5}, \frac{2 \sqrt{5}}{5}\right)$，对应的直线为 $y=\frac{1}{2}x, y=x, y=2x$（见图）。每份蛋糕的面积为 $6$ 平方拜托米。

附加样例

1. $n=6, k=1$，蛋糕为倒 L 形，切割后某部分不连通。
2. $n=4, k=300000$，蛋糕为正方形。
3. $n=300000, k=1$，蛋糕关于直线 $x=y$ 对称。

数据范围与提示

详细子任务附加限制及分值如下表所示。