题目描述

题目译自 JOISC 2025 Day4 T1 「電子回路 2 / Circuit 2」

JOI 君正在玩一套电子电路玩具。这套玩具包含 $N$ 个 AND 元件、$N$ 个 OR 元件以及一个电路板。电路板上有 $2N+1$ 个开关和 $N$ 个元件插槽，你可以将 AND 或 OR 部件插入插槽使用。电路板根据安装的元件和开关状态，以以下方式输出 $0$ 或 $1$ 的值。

• 开关编号从 $0$ 到 $2N$，每个开关有 ON 或 OFF 两种状态。每个开关按以下规则输出 $0$ 或 $1$。
• 元件插槽编号从 $0$ 到 $N-1$，每个插槽按以下规则输出 $0$ 或 $1$。
• 各开关和元件插槽的输出按编号从大到小（相同编号时元件插槽优先）的顺序确定，规则如下：
  • 对于 $j=2N, 2N-1, \ldots, N$，开关 $j$ 输出：
    • 若开关 $j$ 为 OFF，则输出 $0$。
    • 若开关 $j$ 为 ON，则输出 $1$。
  • 对于 $j=N-1, N-2, \ldots, 0$，设元件插槽 $j$ 的输出为 $x$，则开关 $j$ 输出：
    • 若开关 $j$ 为 OFF，则输出 $x$。
    • 若开关 $j$ 为 ON，则输出 $1-x$。
  • 对于 $i=N-1, N-2, \ldots, 0$，元件插槽 $i$ 与两个开关 $U_{i}, V_{i}$ 连接，其中 $i < U_{i} < V_{i} \leq 2N$。设开关 $U_{i}$ 输出为 $x$，开关 $V_{i}$ 输出为 $y$，则元件插槽 $i$ 输出：
    • 若安装的是 AND 元件，则输出 $\min(x, y)$。
    • 若安装的是 OR 元件，则输出 $\max(x, y)$。
  • 对于 $j=1, 2, \ldots, 2N$，恰好存在一个 $i$ $(0 \leq i \leq N-1)$ 使得 $U_{i}=j$ 或 $V_{i}=j$。
  • 电路板的输出与开关 $0$ 的输出相同。

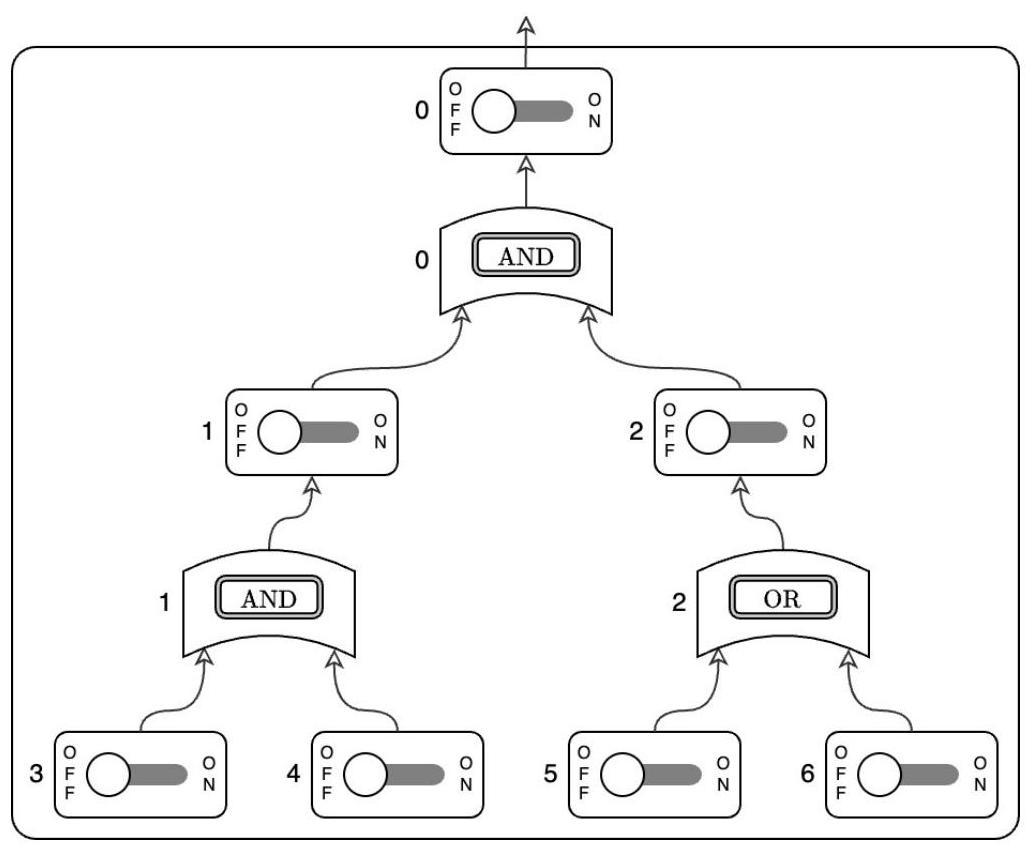
例如，若 $N=3$，$U_{0}=1, V_{0}=2, U_{1}=3, V_{1}=4, U_{2}=5, V_{2}=6$，且元件插槽 $0, 1, 2$ 分别安装了 AND 元件、AND 元件和 OR 元件，则电路板如下图所示：

JOI 君原本打算在所有元件插槽上安装 AND 元件，但发现安装的元件中混入了最多 $R$ 个 OR 元件。由于 AND 元件和 OR 元件外观无法区分，必须通过电路板测试来分辨。你需要通过向 JOI 君提出最多 $1000$ 个以下形式的询问，确定哪些插槽安装了 OR 元件：

• 你可以指示 JOI 君如何设置 $2N+1$ 个开关的状态。JOI 君会按照指示调整开关状态，并告诉你电路板的输出值。

给定电路板的连接信息和安装 OR 元件的上限数量，你需要编写一个程序，通过不超过 $1000$ 次询问，确定哪些元件插槽安装了 OR 元件。

输入格式

你需要提交一个文件，文件名为 circuit.cpp。需通过 #include 引入 circuit.h，并实现以下函数：

• std::string solve(int N, int R, std::vector<int> U, std::vector<int> V)
  • 此函数在每个测试点中仅调用一次。
  • 参数 N 是元件插槽数量 $N$。
  • 参数 R 是安装 OR 元件的个数上限 $R$。
  • 参数 U, V 是长度为 $N$ 的数组，对于 $0 \leq i \leq N-1$，U[i], V[i] 表示元件插槽 $i$ 连接的开关编号 $U_{i}, V_{i}$。
  • 此函数必须返回一个长度为 $N$ 的字符串 t，由字符 & 和 | 组成，满足：
    • 对于每个 $i=0, 1, \ldots, N-1$，若元件插槽 $i$ 安装的是 AND 元件，则 t[i] 为 &；若为 OR 元件，则 t[i] 为 |。
  • 若返回的 t 长度不等于 $N$，将被判为 Wrong Answer [1]。
  • 若返回的 t 包含非 & 或 | 的字符，将被判为 Wrong Answer [2]。
  • 若返回的 t 与实际安装元件种类不符，将被判为 Wrong Answer [3]。

你的程序可以调用以下函数：

• int query(std::string s)
  • 此函数用于向 JOI 君提出询问。
  • 参数 s 是一个长度为 $2N+1$ 的字符串，由字符 0 和 1 组成。对于 $j=0, 1, \ldots, 2N$，若 s[j] 为 0，表示将开关 $j$ 设置为 OFF；若为 1，表示设置为 ON。
  • 若参数 s 的长度不等于 $2N+1$，将被判为 Wrong Answer [4]。
  • 若参数 s 包含非 0 或 1 的字符，将被判为 Wrong Answer [5]。
  • 此函数调用次数不得超过 $1000$ 次，否则将被判为 Wrong Answer [6]。
  • 函数返回值是在参数 s 设置下的电路板输出值。

注意事项

• 你可以自由实现其他内部函数或声明全局变量。
• 你的程序不得以任何方式与标准输入、标准输出或其他文件进行交互，但允许向标准错误输出调试信息。

实际评测程序非自适应，答案固定。

编译与运行

「文件」界面提供示例评测程序压缩包。该压缩包也包含需提交的文件样例。

示例评测程序由一个文件组成，文件名为 grader.cpp。要测试你的程序，请将 grader.cpp, circuit.cpp, circuit.h 放入同一目录，并执行以下命令：

g++ -std=gnu++20 -O2 -o grader grader.cpp circuit.cpp

或者，你可以使用压缩包中包含的 compile.sh 文件，执行以下命令：

./compile.sh

编译成功后，将生成名为 grader 的可执行文件。

注意，实际评分程序与样例评分程序可能不同。示例评测程序作为单一进程启动，从标准输入读取输入，并将结果输出到标准输出。

输入格式

设 $T$ 为函数 solve 应返回的长度为 $N$ 的字符串。示例评测程序从标准输入读取以下格式的数据：

• 第一行包含两个整数 $N, R$，用空格分隔，分别表示元件插槽数量 $N$ 和 OR 元件个数上限 $R$。
• 接下来 $N$ 行，第 $i$ $(0 \leq i \leq N-1)$ 行包含两个整数 $U_{i}, V_{i}$，用空格分隔，表示元件插槽 $i$ 连接的开关编号。
• 最后一行包含一个字符串 $T$，表示实际安装的元件种类。

输出格式

示例评测程序向标准输出输出以下信息：

• 若正确，输出类似 Accepted: 22，其中数字为函数 query 的调用次数。
• 若不正确，输出类似 Wrong Answer [4]，表示不正确答案的类型编号。

示例评测程序在检测到任何不正确条件时会终止执行。若程序符合多个不正确条件，仅显示其中一种。

1 1
1 2
|

在第 $1$ 次 query 调用中，电路板的输出计算如下：

• 开关 $1, 2$ 的状态分别为 ON, OFF，因此开关 $1, 2$ 分别输出 $1, 0$。
• 元件插槽 $0$ 安装了 OR 元件，连接的开关 $1, 2$ 分别输出 $1, 0$，因此元件插槽 $0$ 输出 $\max(1, 0)=1$。
• 开关 $0$ 的状态为 OFF，元件插槽 $0$ 输出为 $1$，因此开关 $0$ 输出 $1$。
• 因此，电路板输出为 $1$。

此样例满足所有子任务的限制。

3 3
1 2
3 4
5 6
&&|

此样例对应问题中的图。

这个样例满足子任务 $3,6,7,8,9$ 的限制。

数据范围与提示

对于所有输入数据，满足：

• $1 \leq N \leq 8000$
• $1 \leq R \leq \min(N, 120)$
• $i < U_i < V_i \leq 2N$ $(0 \leq i \leq N-1)$
• 每个 $j = 1, 2, \ldots, 2N$ 恰被一个 $U_i$ 或 $V_i$ 使用

详细子任务附加限制及分值如下表所示。