题目描述

题目译自 XXVI Olimpiada Informatyczna – II etap Osiedla

比特城频发交通事故，市长认为原因是 $m$ 条双向街道连接 $n$ 个交叉口的网络过于复杂。他决定将每条街道改为单向，以简化交通。

市长希望此举形成尽可能少的社区。社区定义为一个最大（不可扩展）的交叉口集合，其中从任一交叉口可沿单向街道到达该集合内其他任一交叉口。

你的任务是编写程序，确定最少社区数量及对应的街道单向设置。

输入格式

第一行包含两个整数 $n, m$ $(2 \leq n \leq 1000000, 1 \leq m \leq 1000000)$，分别表示交叉口数和街道数。交叉口编号为 $1$ 至 $n$。

接下来的 $m$ 行描述街道，第 $i$ 行包含两个整数 $a_i, b_i$ $(1 \leq a_i, b_i \leq n, a_i \neq b_i)$，表示第 $i$ 条街道连接交叉口 $a_i$ 和 $b_i$。同一对交叉口可能有多条街道。

输出格式

第一行输出一个整数，表示最优单向设置下的社区数量。

第二行输出一个长度为 $m$ 的字符串，表示最优单向设置；第 $i$ 个字符指定第 $i$ 条街道的方向：> 表示从 $a_i$ 到 $b_i$，< 表示从 $b_i$ 到 $a_i$。仅允许使用 > 和 <。若存在多种最优设置，输出任意一种。

7 7
1 2
1 3
2 3
3 4
4 5
4 5
7 6

4
><>>><<

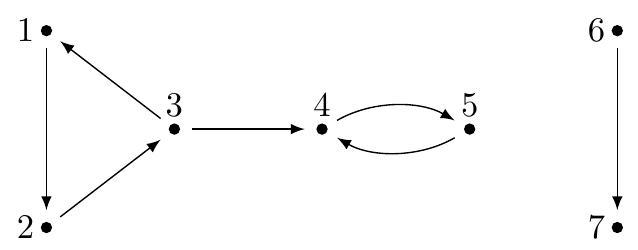
图中展示了一种最优单向设置，形成四个社区，交叉口集合为 $\{1,2,3\}, \{4,5\}, \{6\}, \{7\}$。例如，虽然可从交叉口 $3$ 到达 $4$，但因无法从 $4$ 回到 $3$，它们不属同一社区。

附加样例

1. $n=7, m=10$，小型正确性样例。
2. $n=5000, m=4999$，路径结构（对每个交叉口 $i=1, \ldots, n-1$，有街道连接 $i$ 和 $i+1$）。
3. $n=2000, m=20000$，十倍循环（每个交叉口 $i$ 与 $(i+1) \bmod n$ 间恰有十条街道）。
4. $n=500000, m=999998$，对每个交叉口 $i=1, \ldots, n-2$，有街道连接 $i$ 与 $i+1$ 和 $i+2$；另有两条街道连接 $n-1$ 与 $n$。

数据范围与提示

若输出中只有一行正确，仍可获 $50\%$ 的分数。若要让第二行正确，需输出两行，第一行必须为 32 位整数（int 类型）。

详细子任务附加限制及分值如下表所示。