#HK5089. 「POI2019 R3」长途旅行 Long travels
「POI2019 R3」长途旅行 Long travels
题目描述
题目译自 XXVI Olimpiada Informatyczna – III etap Długie podróże
Bajtazar 在 25 年的信息学奥赛中结识了许多朋友,足迹遍布拜托城。然而,他的朋友分散在各地,探访颇为不易。拜托城有 个城市,通过 条双向航线连接,网络设计确保任意两城市间可达(通常需换乘)。
根据新交通法,每条航线票价固定为 。Bajtazar 提出 个问题:「从朋友所在城市 飞到城市 需要多少费用?」你希望帮助他规划最便宜的路线。
你注意到,Bajtazar 询问的朋友相距甚远,最短路线至少需 次飞行。回答他的查询,助他在下届奥赛前探访所有朋友!
输入格式
第一行包含三个整数 $(2 \leq n \leq 100000, n-1 \leq m \leq 200000, 1 \leq p \leq 200000)$,分别表示城市数、航线数和查询数。城市编号为 至 。
接下来的 行描述航线,第 行包含两个整数 ,表示城市 和 间有双向航线。每条航线至多描述一次。
接下来的 行描述查询,第 行包含两个整数 ,表示从城市 到 的最短飞行次数查询。保证每条路线费用至少 。
输出格式
输出 行,第 行包含一个整数,表示第 个查询的最短飞行次数。
6 7 2
1 2
2 4
3 1
3 4
4 5
4 6
6 5
2 5
1 6
2
3
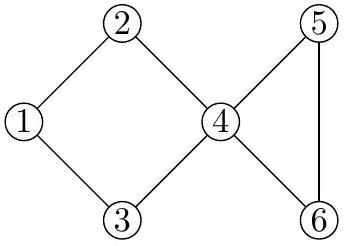
从城市 到 的最短路线为 ,需 次飞行。从城市 到 的最短路线为 ,需 次飞行。
附加样例
- 。
- ,航线形成环。
- ,航线形成两个相接的环。
数据范围与提示
详细子任务附加限制及分值如下表所示。
| 子任务 | 附加限制 | 分值 |
|---|---|---|
| ,每城市至多有 条航线 | ||
| 城市 仅与 有航线 | ||
| 无附加限制 |