题目描述

题目译自 XVI OI Olimpiada Informatyczna – II etap Wyspy na trójkątnej sieci

三角网由边长为 $1$ 的正三角形构成（见题目末尾插图）。在三角网上，路径定义为由边长 $1$ 的三角形组成的有限序列，其中相邻两三角形共享一条边。

由有限个三角网三角形顶点构成的图形称为岛屿，若其中任意两三角形可通过仅包含该图形内三角形的路径连接。

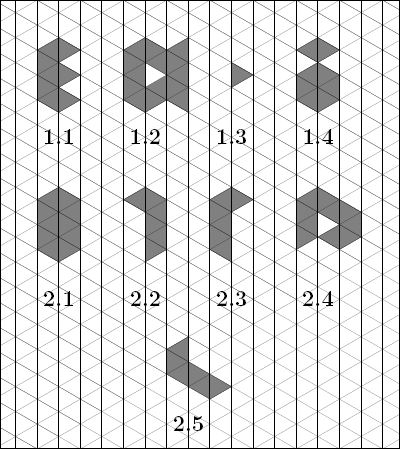
图 1.1、1.2、1.3 所示图形为岛屿，图 1.4 所示图形非岛屿。图 2.2、2.3、2.5 所示图形为同构（即形状相同）。

我们计划为每个 $n \leq 10$ 系统性地描述由 $n$ 个边长 $1$ 三角形构成的所有非同构岛屿，并计算其数量。

由最多 $10$ 个三角形构成的岛屿，其边界为由单位长度网格段组成的闭合折线，可一次性描画（不抬笔，覆盖每段恰一次，回到起点）。描画时可能需多次经过同一顶点（见图 2.4）。对于此类岛屿，不会出现如图 1.2 所示边界分裂为不连通部分的不可一次性描画情况。

描画边界时，每段单位长度后执行以下类型转角：

• a：向左 $120$ 度；
• b：向左 $60$ 度；
• c：$0$ 度（即无转角）；
• d：向右 $60$ 度；
• e：向右 $120$ 度。

每个岛屿边界描画可用由集合 $\{a, b, c, d, e\}$ 中字母组成的单词描述，记录每段单位长度后的转角类型。单词长度等于边界折线的单位段数，包含最后一段后的转角（虽非必要，但便于转换到从不同起点开始的描画描述）。

例如：

• 单词 cdddcddd, dcdddcdd, cbbbcbbb 描述图 2.1 不同描画。
• 单词 cbeddcde, adcabcbb, abcbbadc 描述图 2.2 不同描画。
• 单词 acdabbcb, cddebced 描述图 2.3 不同描画。

若描画边界时岛屿内部始终在右侧，则称此描画为右旋。

对于每座岛屿，可确定其所有同构岛屿及其右旋描画集合。岛屿的编码定义为：

1. 描述某同构岛屿右旋描画的单词；
2. 在满足条件 1 的所有单词中，选择字典序最小的那个。

例如，图 2.2 和 2.3 的岛屿同构，右旋描画包括：

• beddcdec, eddcdecb, ddcdecbe, dcdecbed, cdecbedd, decbeddc, ecbeddcd, cbeddcde；
• bcedcdde, cedcddeb, edcddebc, dcddebce, cddebced, ddebcedc, debcedcd, ebcedcdd。

其编码为字典序最小的 bcedcdde。图 2.4 岛屿编码为 aadecddcddde。

编写程序，完成以下任务：

• 给定尺寸 $k$ 的岛屿编码，生成通过添加一个三角形得到的所有尺寸 $k+1$ 岛屿的编码。
• 给定整数 $n$，生成所有尺寸 $n$ 岛屿的编码。

输入格式

第一行包含整数 $t$ $(1 \leq t \leq 5)$，表示查询数。

接下来的 $t$ 行每行描述一个查询，分为两类：

• 第一类：字母 K 和一个最多由 $9$ 个三角形构成的岛屿编码，用单空格分隔。
• 第二类：字母 N 和整数 $n$ $(1 \leq n \leq 10)$，用单空格分隔。

输出格式

按顺序输出各查询的答案。

对于第一类查询：

• 第一行：可通过添加一个三角形从给定编码的同构岛屿生成的異なる编码数。
• 第二行：所有这些编码，按字典序排列，用单空格分隔。

对于第二类查询：

• 第一行：由 $n$ 个三角形构成的不同的岛屿编码数。
• 第二行：所有这些编码，按字典序排列，用单空格分隔。

2
K adeccecced
N 5

5
acedccecced addebcecced adebebecced adecbedcced cceccecce
4
aedddde bdecdde bececde ccedcde