题目描述

题目译自 JOISC 2013 Day1 T1 「バスの乗り継ぎ」

在 JOI 市，公共交通系统非常发达。尤其值得一提的是，这里的公交专用道路呈棋盘状布局，公交车不会受到交通状况的影响，能够以恒定的速度运行。南北方向的公交专用道路共有 $W$ 条，间隔 $1$ 公里；东西方向的公交专用道路共有 $H$ 条，同样间隔 $1$ 公里。所有公交车都沿着长方形的路线顺时针行驶，速度为每分钟 $1$ 公里。此外，每个公交专用道路的交叉点都设有公交站点。

JOI 君今天原本计划去看一场板球比赛，可惜他睡过头了。虽然可能已经赶不上比赛的开场，但他仍然希望尽可能多地观看比赛，因此想尽快到达比赛场地。

JOI 君事先已经查好了公交车的运行信息，了解了每辆公交车的当前位置以及它们的运行路线。你的任务是编写一个程序，计算 JOI 君现在立即出发，通过换乘公交车，到达比赛场地所需的最短时间。需要注意的是，移动只能依靠公交车完成，并且由于换乘公交车需要时间，JOI 君无法在下车的同时立刻换乘到同一交叉点停靠的其他公交车，必须在下车后至少等待 $1$ 分钟，才能搭乘随后到达的公交车。此外，题目保证 JOI 君一定能够通过公交车到达目的地。

输入格式

从标准输入中读取以下数据：

• 第 $1$ 行包含 $6$ 个整数 $W, H, S_{X}, S_{Y}, G_{X}, G_{Y}$ $\left(1 \leq S_{X} \leq W, 1 \leq S_{Y} \leq H, 1 \leq G_{X} \leq W, 1 \leq G_{Y} \leq H\right)$，依次用空格分隔。这表示南北方向的公交专用道路有 $W$ 条，东西方向的公交专用道路有 $H$ 条。JOI 君的初始位置位于西侧第 $S_{X}$ 条公交专用道路与北侧第 $S_{Y}$ 条公交专用道路的交叉点，而他的目的地——比赛场地——位于西侧第 $G_{X}$ 条公交专用道路与北侧第 $G_{Y}$ 条公交专用道路的交叉点。JOI 君的初始位置与目的地不同，并且他出发时初始位置不会有公交车停靠。
• 第 $2$ 行包含一个整数 $N$，表示 JOI 市运行的公交车总数。
• 接下来的 $N$ 行，每行描述一辆公交车的信息。第 $i$ 行的 $5$ 个整数 $X_{1i}, Y_{1i}, X_{2i}, Y_{2i}, T_{i}$ $\left(1 \leq X_{1i} < X_{2i} \leq W, 1 \leq Y_{1i} \leq Y_{2i} \leq H, 0 \leq T_{i} < 2 \times (X_{2i} - X_{1i} + Y_{2i} - Y_{1i})\right)$ 表示：第 $i$ 辆公交车的路线西北端位于西侧第 $X_{1i}$ 条道路与北侧第 $Y_{1i}$ 条道路的交叉点，东南端位于西侧第 $X_{2i}$ 条道路与北侧第 $Y_{2i}$ 条道路的交叉点。JOI 君出发时，这辆公交车已从西北端顺时针行驶了 $T_{i}$ 公里。

输出格式

在标准输出中，输出一行一个整数，表示 JOI 君从出发到到达比赛场地所需的最短时间。

10 10 1 3 10 1
3
1 3 5 6 4
5 5 7 10 1
7 1 10 5 9

50

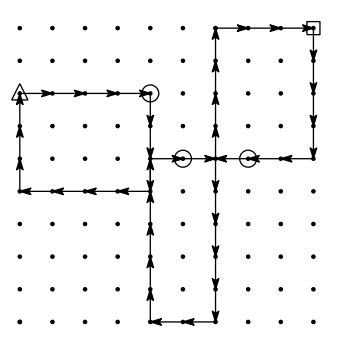
上图展示了 JOI 市从空中俯瞰的情景，圆圈表示公交车的当前位置，箭头表示公交车的运行路线。JOI 君的起点用三角形标记，目的地比赛场地用矩形标记。

JOI 君需要等待第 $1$ 号公交车到来。假设在出发后 $10$ 分钟他登上第 $1$ 号公交车，那么在 $11$ 分钟后，情况如下图所示。

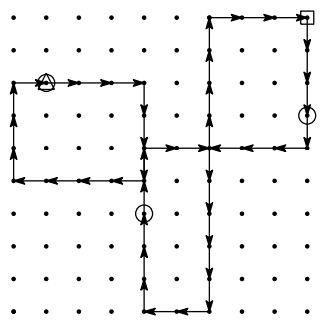
随后，JOI 君需要从第 $1$ 号公交车换乘到第 $2$ 号公交车。假设在出发后 $16$ 分钟他下车，那么到 $19$ 分钟时，情况如下图所示。

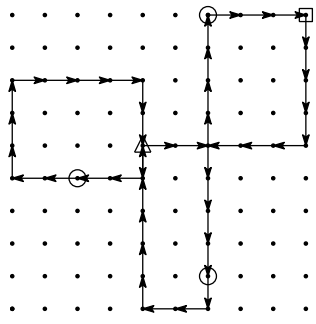
接着，他登上第 $2$ 号公交车后，需要换乘到第 $3$ 号公交车。假设在出发后 $29$ 分钟他从第 $2$ 号公交车下车，此时第 $3$ 号公交车刚好停在同一交叉点，但由于换乘需要 $1$ 分钟，他无法立即登上这辆车。

直到出发后 $43$ 分钟，JOI 君登上第 $3$ 号公交车，在 $49$ 分钟时，情况如下图所示，接近比赛场地。

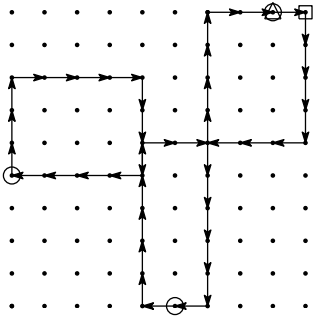
再过 $1$ 分钟，即出发后 $50$ 分钟，JOI 君到达比赛场地。更快到达是不可能的，因此程序应输出 $50$。

4 3 2 1 4 3
3
1 1 4 2 0
1 1 2 2 3
2 2 4 3 3

6

数据范围与提示

对于所有输入数据，满足：

• $2 \leq W \leq 1000$
• $2 \leq H \leq 1000$
• $1 \leq N \leq 1000$

详细子任务附加限制及分值如下表所示。