题目描述

题目译自 JOISC 2013 Day1 T4 「JOI ポスター」

K 理事长正在设计三张用于支持日本国际信息奥林匹克代表队的海报。每张海报计划分别融入一个字母：J、O 或 I。K 理事长已经完成了带有字母 J 和 I 的海报，现在他打算以澳大利亚的星空为背景，设计带有字母 O 的海报。

海报是一个宽度为 $W$、高度为 $H$ 的长方形区域，左下角坐标为 $(0,0)$，右上角坐标为 $(W, H)$。海报上印有 $N$ 颗星星。第 $i$ 颗星星 $S_{i}$ $(1 \leq i \leq N)$ 在海报上的坐标为 $(X_{i}, Y_{i})$，且任意两颗星星不会位于相同坐标。

在设计字母 O 时，K 理事长有如下构想：从 $N$ 颗星星中选出不同的 $4$ 颗，分别命名为 $A, B, C, D$。以 $A$ 为圆心、经过 $B$ 的圆称为圆 $O_{1}$，以 $C$ 为圆心、经过 $D$ 的圆称为圆 $O_{2}$。当这两个圆 $O_{1}$ 和 $O_{2}$ 满足以下两个条件时，这 $4$ 颗星星 $A, B, C, D$ 即可作为 K 理事长的设计候选：

• 圆 $O_{1}$ 完全包含圆 $O_{2}$，即圆 $O_{2}$ 内部或圆周上的任意一点都在圆 $O_{1}$ 的内部（不包括圆 $O_{1}$ 的圆周）。
• 两个圆均不超出海报的长方形区域，即圆内部或圆周上的任意一点 $(X, Y)$ 满足 $0 \leq X \leq W$ 且 $0 \leq Y \leq H$。

那么，符合 K 理事长设计候选条件的 $4$ 颗星星 $A, B, C, D$ 的选择方式总共有多少种呢？

给定海报的尺寸和星星的信息，你需要编写一个程序，计算符合 K 理事长设计候选条件的 $4$ 颗星星 $A, B, C, D$ 的选择方式有多少种。

输入格式

从标准输入中读取以下数据：

• 第一行包含三个整数 $N, W, H$，用空格分隔，分别表示海报上印有的星星数量、海报的宽度和高度。
• 接下来 $N$ 行中，第 $i$ $(1 \leq i \leq N)$ 行包含两个整数 $X_{i}, Y_{i}$ $(0 \leq X_{i} \leq W, 0 \leq Y_{i} \leq H)$，用空格分隔，表示星星 $S_{i}$ 在海报上的坐标。

输出格式

在标准输出中输出一行一个整数，表示符合 K 理事长设计候选条件的 $4$ 颗星星 $A, B, C, D$ 的选择方式总数。

7 20 15
9 5
13 9
15 13
7 4
6 8
14 7
16 7

3

此输入样例对应问题描述中的图示。星星 $S_{i}$ 用点 $i$ 表示。

在此图中，符合 K 理事长设计候选条件的 $4$ 颗星星 $A, B, C, D$ 的选择方式有 $3$ 种。每种情况下的圆 $O_{1}$ 和 $O_{2}$ 如问题描述中的图示所示。

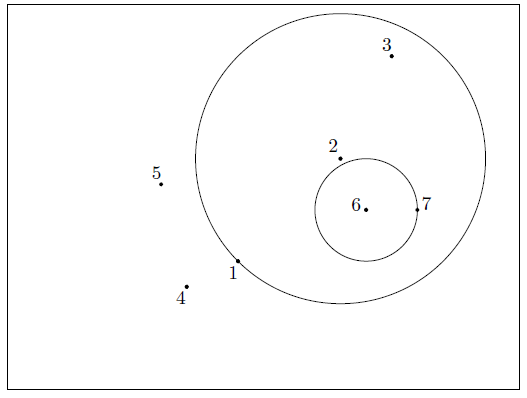
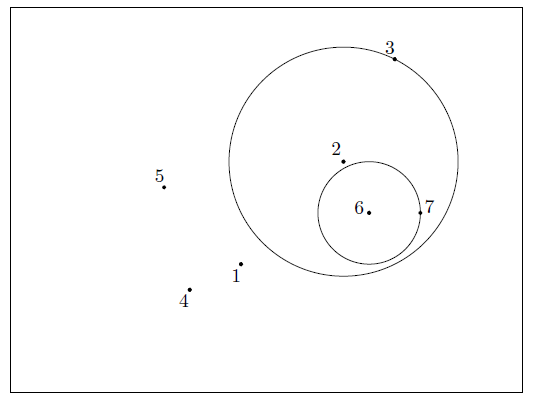
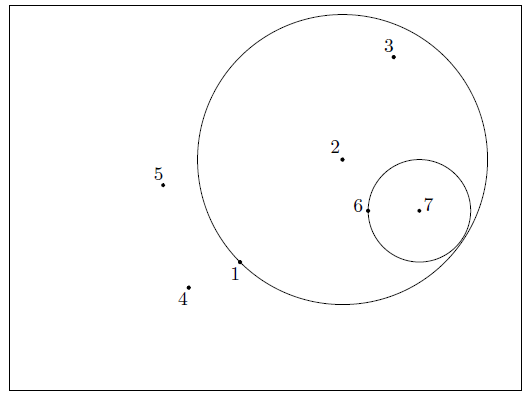
注意，在第三种情况中，圆 $O_{1}$ 和圆 $O_{2}$ 并不接触。

15 20 30
11 8
14 25
3 20
1 27
2 16
12 8
0 4
3 10
12 11
5 9
16 3
2 13
4 24
18 3
12 28

12

数据范围与提示

对于所有输入数据，满足：

• $4 \leq N \leq 50$
• $1 \leq W \leq 1000$
• $1 \leq H \leq 1000$
• $0 \leq X_{i} \leq W$
• $0 \leq Y_{i} \leq H$
• 任意两颗星星不位于相同坐标。

详细子任务附加限制及分值如下表所示。