题目描述

题目译自 JOISC 2013 Day3 T1 「ケーキの切り分け」

JOI 君和 IOI 酱是双胞胎兄妹。JOI 君最近迷上了甜点制作，今天他又烤了一块蛋糕准备享用，可刚烤好，闻到香味的 IOI 酱就跑来了，于是两人决定一起分享这块蛋糕。

蛋糕是圆形的，从某个点开始沿放射状切开，将蛋糕分成 $N$ 块扇形小片，并按逆时针顺序从 $1$ 到 $N$ 编号。也就是说，对于 $1 \leq i \leq N$，第 $i$ 块小片与第 $i-1$ 块和第 $i+1$ 块相邻（其中第 $0$ 块视为第 $N$ 块，第 $N+1$ 块视为第 $1$ 块）。第 $i$ 块小片的大小为 $A_{i}$，由于切分技术非常拙劣，每块 $A_{i}$ 的值都不相同。

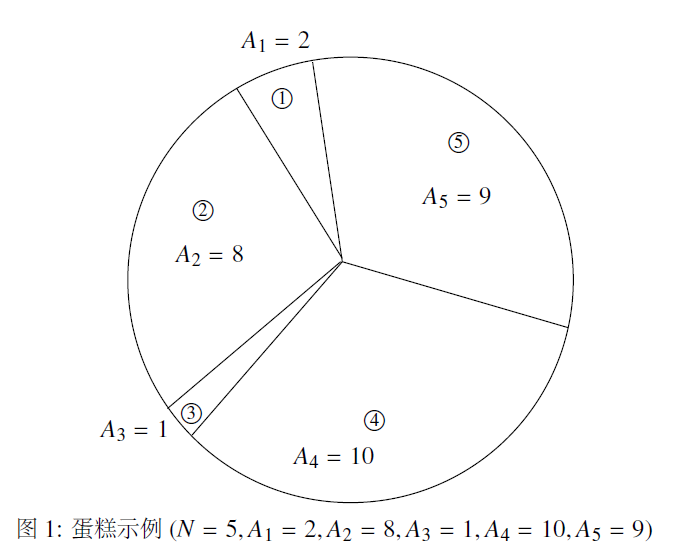
这 $N$ 块蛋糕将由 JOI 君和 IOI 酱分着吃，分法如下：

• 首先，JOI 君从 $N$ 块中选择一块取走。
• 随后，从 IOI 酱开始，两人轮流从剩余的小片中各取一块。但由于两人都不擅长取蛋糕（为了不弄塌蛋糕），只能选择两侧相邻小片中至少有一块已被取走的小片。如果有多块符合条件的小片，则选择其中最大的一块取走。

JOI 君想知道，对于每一块小片，如果他最先取走这块，最终他能拿到的所有小片大小之和是多少。

给定蛋糕小片数量 $N$ 以及 $N$ 块小片的大小信息，你需要编写一个程序，计算对于每一块小片，若 JOI 君最先取走该片，最终他能拿到的所有小片大小之和。

输入格式

从标准输入中读取以下数据：

• 第一行包含一个整数 $N$，表示蛋糕被切分成 $N$ 块小片。
• 接下来 $N$ 行中，第 $i$ $(1 \leq i \leq N)$ 行包含一个整数 $A_{i}$，表示第 $i$ 块小片的大小为 $A_{i}$。

输出格式

在标准输出中输出 $N$ 行，第 $i$ $(1 \leq i \leq N)$ 行输出一个整数，表示若最先取走第 $i$ 块小片，JOI 君最终拿到的所有小片大小之和。

5
2
8
1
10
9

13
18
12
13
12

此样例对应问题描述中的图示。

例如，若最先取走第 $1$ 块小片：

• 剩余小片中，符合“两侧相邻小片至少有一块已被取走”条件的是第 $2$ 块和第 $5$ 块，第 $5$ 块较大，因此接下来取走第 $5$ 块。
• 同样，接下来比较第 $2$ 块和第 $4$ 块，第 $4$ 块较大，取走第 $4$ 块。
• 接下来比较第 $2$ 块和第 $3$ 块，第 $2$ 块较大，取走第 $2$ 块。
• 最后只剩第 $3$ 块，取走第 $3$ 块。

取走顺序为：

JOI 君取走第 $1$ 块、第 $4$ 块和第 $3$ 块，总大小为 $13$，因此第一行输出 $13$。对于其他小片作为首选的情况，也按此方式计算。

数据范围与提示

对于所有输入数据，满足：

• $2 \leq N \leq 300000$
• $1 \leq A_{i} \leq 1000000000$ $(1 \leq i \leq N)$

详细子任务附加限制及分值如下表所示。