注意事项

在 LibreOJ 上，由于语言限制，目前只支持以下语言的提交：

• C++（标准为 C++ 11 及以上）

请在提交源代码前添加 #include "shortcut.h"。

题目描述

Pavel 有一个非常简单的铁路玩具。 它有一条含有 $n$ 个车站的主干线并且连续编号为 $0$ 到 $n - 1$ 。车站 $0$ 和车站 $n - 1$ 就在这条主干线的两端。 其中车站 $i$ 和车站 $i + 1$ 之间的距离为 $l_i$ 厘米（$0 \leq i < n - 1$）。

除了这条主干线之外，这个铁路也许会有些支线。每条支线都是由主干线中的一个车站和主干线外的一个新车站之间的一条新铁路构成（这些新的车站不会被编号）。在主干线中的一个车站最多只能有一条支线。以主干线中的车站 $i$ 为起点的支线的长度为 $d_i$ 厘米。我们用 $d_i = 0$ 来表示车站 $i$ 没有支线。

Pavel 现正规划一条快捷方式：一条在主干线中两个不相同的车站之间（它们可能相邻）的快速干线。这条快速干线无论是连接哪两个车站，它的长度都将会恰好是 $c$ 厘米。

铁路中的每一段，包括那条新的快速干线，都能够双向行驶。任意两个车站的距离就是它们之间沿着铁路由一个车站到另一个车站之间最短路径的长度。所有车站组合中最大的距离就叫做整个铁路网络的直径。换句话说，存在一个最小值 $t$ 使任意两个车站之间的距离都不会超过 $t$。

Pavel 就是想建造一条快速干线，使得有了这条快速干线后新的铁路网络的直径能达到最小值。

程序实现细节

你应该实现如下函数：

int64 find_shortcut(int n, int[] l, int[] d, int c)

• n：主干线中的车站数目，
• l：主干线中车站之间的距离（数组的长度为 $n - 1$），
• d：支线的长度（数组的长度为 $n$），
• c：新快速干线的长度。

函数应该返回加入新快速干线后铁路网络直径的最小可能值。

请使用提供的模板文件，参考关于你所使用的编程语言的实现细节。

样例 1

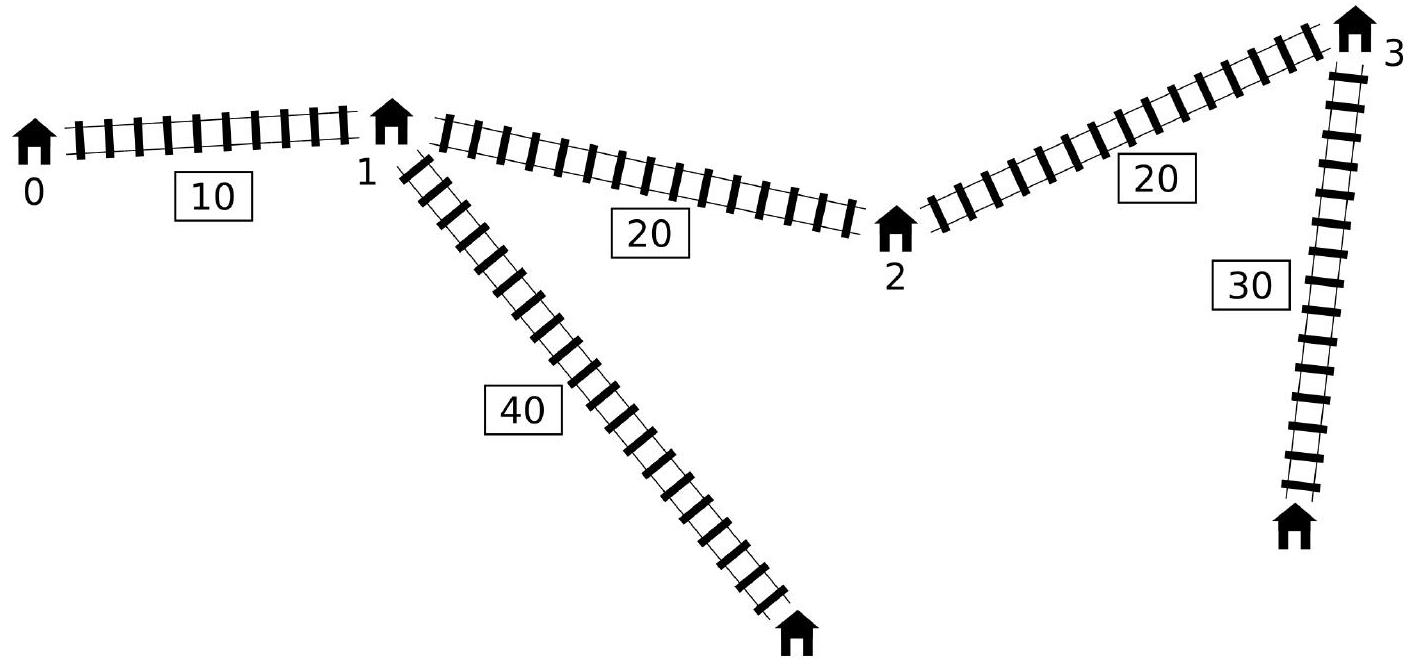
对于上图所示的铁路网络，样例评分程序会调用以下函数：

find_shortcut(4, [10, 20, 20], [0, 40, 0, 30], 10)

最优解是在车站 $1$ 和车站 $3$ 之间建造一条快速干线，如下图所示。

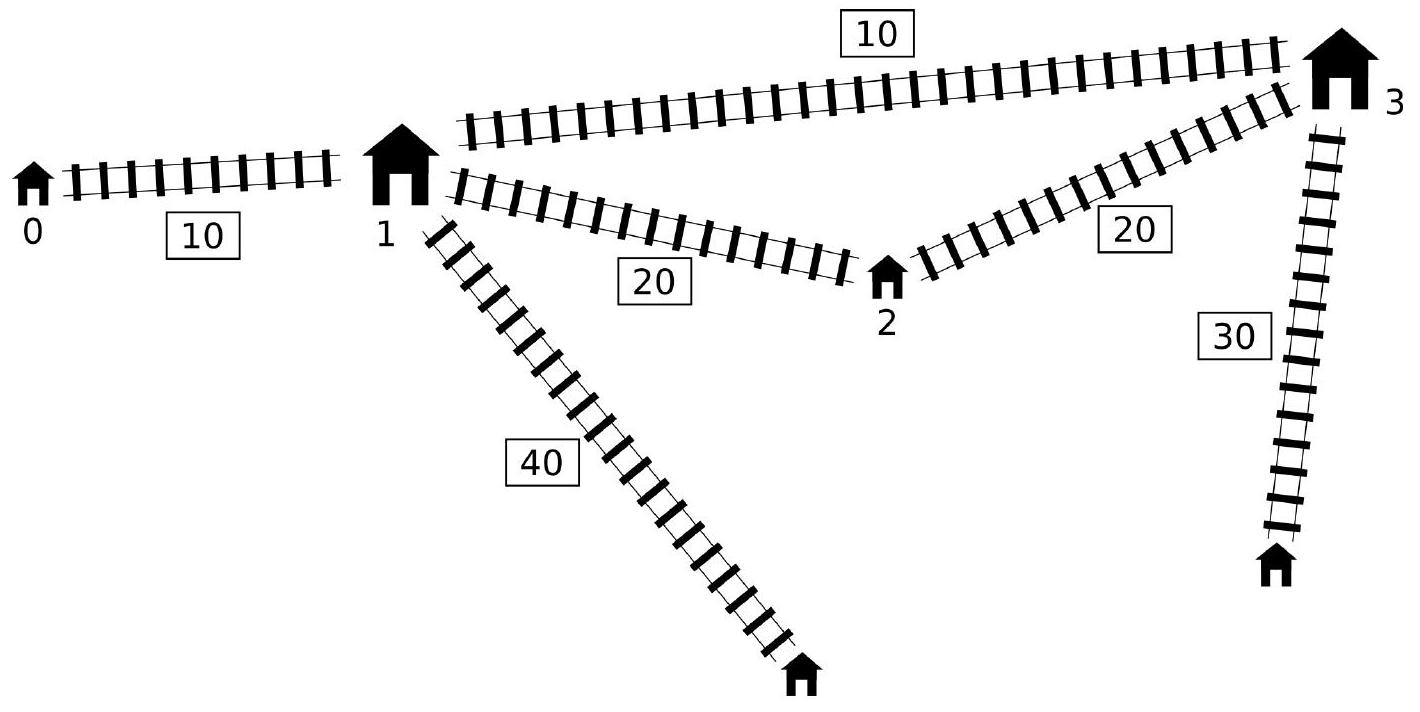
这个新铁路网络的直径是 $80$ 厘米，所以函数应该返回数值 $80$。

样例 2

样例评分程序会调用以下函数：

find_shortcut(9, [10, 10, 10, 10, 10, 10, 10, 10], [20, 0, 30, 0, 0, 40, 0, 40, 0], 30)

最优解是连接车站 $2$ 和车站 $7$，这个解的直径是 $110$。

样例 3

样例评分程序会调用以下函数：

find_shortcut(4, [2, 2, 2], [1, 10, 10, 1], 1)

最优解是连接车站 $1$ 和车站 $2$ , 这样直径将被缩短到 $21$.

样例 4

样例评分程序会调用以下函数：

find_shortcut(3, [1, 1], [1, 1, 1], 3)

在任意两个车站中建立长度为 $3$ 的快速干线都不会改进整个铁路网络的直径，因此其直径仍为初始值 $4$。

子任务

在所有子任务中 $2 \leq n \leq 1\,000\,000$，$1 \leq l_i \leq 10^9$，$0 \leq d_i \leq 10^9$，$1 \leq c \leq 10^9$。

1. （9 分）$2 \leq n \leq 10$，
2. （14 分）$2 \leq n \leq 100$，
3. （8 分）$2 \leq n \leq 250$，
4. （7 分）$2 \leq n \leq 500$，
5. （33 分）$2 \leq n \leq 3000$，
6. （22 分）$2 \leq n \leq 100\,000$，
7. （4 分）$2 \leq n \leq 300\,000$，
8. （3 分）$2 \leq n \leq 1\,000\,000$。

样例评测程序

样例评测程序按照以下格式读入输入：

• 第 1 行：整数 $n$ 和 $c$，
• 第 2 行：整数 $l_0, l_1, \ldots, l_{n-2}$，
• 第 3 行：整数 $d_0, d_1, \ldots, d_{n-1}$。