题目描述

译自 ROI 2015 Day1 T2. Памятник

阿尔汉格尔斯克市中心的一个广场铺满了尺寸为 $1 \times k$ 的矩形瓷砖。如果引入一个坐标系，使得其中一块瓷砖的左下角坐标为 $(0, 0)$，那么所有瓷砖的左下角坐标将为 $(i \cdot k + j, j)$，其中 $i$ 和 $j$ 为整数。

广场上决定为著名的阿尔汉格尔斯克作家兼艺术家斯捷潘·皮萨霍夫（Stepan Pisakhov）树立一座纪念碑。为了安装纪念碑，需要移除所有完全或部分位于纪念碑底座下的瓷砖。纪念碑的底座是一个多边形，其顶点具有整数坐标，且所有边都平行于坐标轴。已知任何一条与坐标轴平行的直线与底座相交时，交集仅为一个线段。

为了安装纪念碑，需要在广场上选择一个位置，使得移除的瓷砖数量最少。选择位置时，仅允许沿坐标轴方向平移底座。 你的任务是编写一个程序，计算出为了放置纪念碑所需移除的最少瓷砖数量。

输入格式

输入数据的第一行包含两个整数 $n$ 和 $k$，分别表示纪念碑底座的顶点数量和瓷砖的尺寸。

接下来的 $n$ 行，每行包含两个整数 $x_i$ 和 $y_i$，表示底座第 $i$ 个顶点的坐标。顶点坐标按逆时针顺序给出。

输出格式

输出一行，包含一个整数，表示为了放置纪念碑所需移除的最少瓷砖数量。

12 3
2 3
1 3
1 2
3 2
3 1
8 1
8 2
10 2
10 3
8 3
8 4
2 4

7

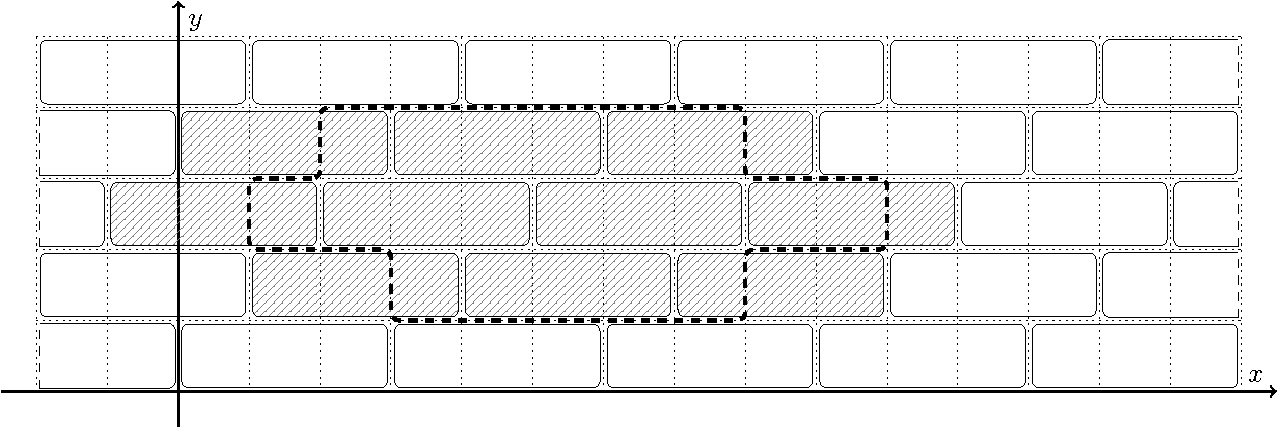
在第一个样例中，纪念碑底座的初始位置如图所示。

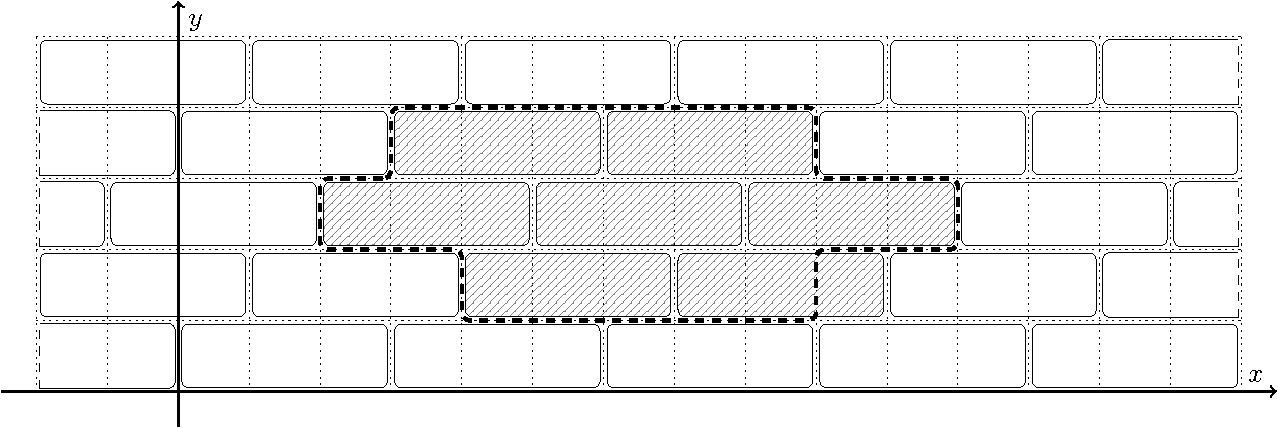
在第一个样例中，纪念碑底座的最优位置如图所示。

数据范围与提示

详细子任务附加限制及分值如下表所示：