题目描述

译自 ROIR 2016 Day2 T1. Три сына

在弗拉特兰国王的领地内，有一条长度为 $n$ 公里的笔直道路，路的一侧是一片广袤的森林。国王深受自然保护理念的影响，决定将这片森林变成自然保护区。然而，他的三个儿子对此表示反对，因为他们希望继承这些土地。

国王有三个儿子：小儿子、中儿子和大儿子。国王决定，森林中将有一部分区域不纳入保护区，而是留给儿子们作为遗产。在制定遗嘱时，国王希望这些土地的划分满足以下条件：

• 每个儿子的土地必须是正方形，且边长为正整数。每个正方形的一条边必须紧靠道路。假设三个儿子的土地边长分别为 $a,b,c$；
• 三个正方形的边长之和必须完全覆盖道路的长度，即 $a + b + c$ 必须等于 $n$；
• 小儿子的土地面积必须严格小于中儿子的土地面积，中儿子的土地面积又必须严格小于大儿子的土地面积，即必须满足不等式 $a < b < c$；
• 三个土地的面积总和 $a^{2} + b^{2} + c^{2}$ 必须尽可能小。

你需要编写一个程序，根据给定的道路长度，确定分配给国王三个儿子的土地的边长。

输入格式

输入文件包含一个整数 $n$ $(6 \leq n \leq 10^{9})$。

输出格式

输出文件应包含三个以空格分隔的正整数：$a, b, c$，分别表示分配给小儿子、中儿子和大儿子的土地的边长。如果存在多个最优解，可以输出任意一个。

6

1 2 3

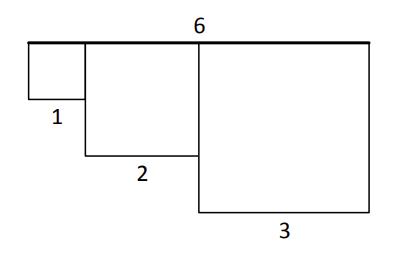
对于输入数据 $n = 6$，最优的土地划分方式是：

• 小儿子得到边长为 $1$ 的正方形土地；
• 中儿子得到边长为 $2$ 的正方形土地；
• 大儿子得到边长为 $3$ 的正方形土地。

这样，边长之和为 $1 + 2 + 3 = 6$，满足覆盖道路的要求；同时，面积总和为 $1^{2} + 2^{2} + 3^{2} = 1 + 4 + 9 = 14$，这是满足条件的最小面积和。

数据范围与提示

详细子任务附加限制及分值如下表所示：