题目描述

题目译自 XXVII Olimpiada Informatyczna – Eliminacje do IOI Unia Bajtopejska

拜托佩亚是拜托西亚星球上的一块大陆，上面分布着许多国家。为了简化问题，这些国家被编号为从 $A$ 到 $B$（包含两端）的连续非负整数。每个编号在这一区间内的国家唯一对应一个国家，而小于 $A$ 或大于 $B$ 的编号则属于其他大陆的国家。拜托佩亚的各国政府认识到，进一步发展需要加强整合，因此他们成立了一个经济和政治联盟，称为「拜托佩亚联盟」。

迄今为止，拜托佩亚各国之间的唯一交通方式是公路连接。现在是时候彻底改变这一现状了：Bengen 区项目计划建立一个航空网络，确保联盟内任意两个国家之间能够实现通信（不一定是直接连接）。

当然，各方一致同意，网络的建设成本应尽可能低。建立国家编号为 $x$ 和 $y$ 之间航空连接的成本为 $x \oplus y$ 拜塔拉尔（bajtalar），其中 $\oplus$ 表示异或操作（XOR）：$x \oplus y$ 的第 $i$ 位为 $1$，当且仅当 $x$ 和 $y$ 的第 $i$ 位中恰好有一个为 $1$。

联盟当局希望在协商 Bengen 区项目细节之前，先了解建设这一网络的成本。请帮助他们，编写一个程序来计算这一成本。

输入格式

输入数据的第一行包含一个自然数 $q$ $(1 \leq q \leq 100000)$，表示数据集的数量。接下来的 $q$ 行中，每行包含一组数据，每组数据由两个非负整数 $A$ 和 $B$ $(0 \leq A \leq B \leq 10^{16})$ 组成，表示各国编号的范围。

输出格式

输出恰好 $q$ 行，第 $i$ 行包含第 $i$ 组数据的答案。每组数据的答案是一个整数，表示建立 Bengen 区的最小可能成本。

1
2 5

8

拜托佩亚的国家编号为 $\{2,3,4,5\}$。只需建立三条航空连接：国家 $2$ 与 $3$ 之间（成本：$2 \oplus 3=1$），国家 $2$ 与 $4$ 之间（成本：$2 \oplus 4=6$），以及国家 $4$ 与 $5$ 之间（成本：$4 \oplus 5=1$）。因此，网络总成本为 $1+6+1=8$ 拜塔拉尔。

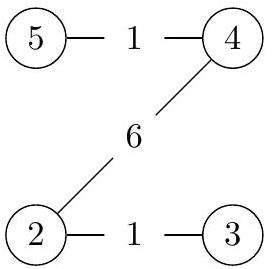
附加样例

1. $q=1$，$A=0$，$B=17$；
2. $q=1$，$A=50000$，$B=200000$；
3. $q=1$，$A=0$，$B=2^{40}$；
4. $q=40$，在第 $i$ 个查询中 $A=2^{i-1}+1$，$B=2^{i}$。

数据范围与提示

详细子任务附加限制及分值如下表所示。