题目描述

题目译自 XXVII Olimpiada Informatyczna – Eliminacje do IOI Reprezentanci firmy

Bajtazar 是 Bajtokom 的老板，这家公司是整个拜托西亚最大的信息技术解决方案供应商。目前，公司正面临严重的财务困境。唯一能避免公司破产的希望是赢得一项非常重要项目的招标，同时（不幸的是）不得不大规模裁员。招标评估的主要标准当然是报价最低。

问题在于，执行该项目需要保留一部分员工，因此不能全部裁员，这意味着必须支付某些人的薪资。Bajtazar 将所有员工排成一个长队。经过详细分析，他决定需要组建几个员工团队。每个团队必须从队伍的一个连续区间中选取，并且人数至少达到一个固定的下限。Bajtazar 了解每个下属的薪资要求，希望确定哪些员工应留下来，以便既能完成项目，又使薪资成本尽可能低。

显然，这项选择任务落在了你的肩上。为了方便你，Bajtazar 确定的团队结构满足以下条件：对于任意两个团队，它们选取员工的区间要么完全不相交，要么一个完全包含在另一个之中。被雇佣的员工可以同时在多个团队中工作（并且只需支付一次薪资！）。

请帮助 Bajtazar 拯救公司！

输入格式

输入数据的第一行包含一个整数 $n$ $(1 \leq n \leq 200000)$，表示员工总数。员工按照队伍顺序编号为从 $1$ 到 $n$。

第二行包含 $n$ 个整数 $c_{i}$ $(1 \leq c_{i} \leq 10^{9})$，其中第 $i$ 个数字表示第 $i$ 个员工的薪资要求。

第三行包含一个整数 $m$ $(1 \leq m \leq 200000)$，表示执行项目所需团队的数量。

接下来的 $m$ 行描述各个团队，每行包含三个整数 $s_{j}, t_{j}, p_{j}$ $(1 \leq s_{j} \leq t_{j} \leq n, 1 \leq p_{j} \leq t_{j}-s_{j}+1)$，表示第 $j$ 个团队应由至少 $p_{j}$ 名员工组成，这些员工必须从队伍中第 $s_{j}$ 到第 $t_{j}$ 个员工（包含两端）的连续区间中选取。

保证输入中所有连续区间都是成对不同的，即团队对应的有序对 $(s_{j}, t_{j})$ 互不相同。此外，对于任意两个区间，要么不相交，要么一个完全包含在另一个之中。

输出格式

第一行输出一个整数，表示所选项目员工的最小薪资成本。

第二行和第三行需输出一个符合此成本的雇佣员工列表示例：第二行输出员工数量 $p$ $(1 \leq p \leq n)$，第三行输出 $p$ 个员工编号的序列。

如果存在多个正确答案，你的程序可以输出其中任意一个。

8
15 8 2 20 4 9 3 10
4
1 8 5
2 4 2
5 6 1
5 8 2

26
5
2 3 6 5 7

在下图中展示了样例的最优解，被圈出的员工是 Bajtazar 雇佣的员工。

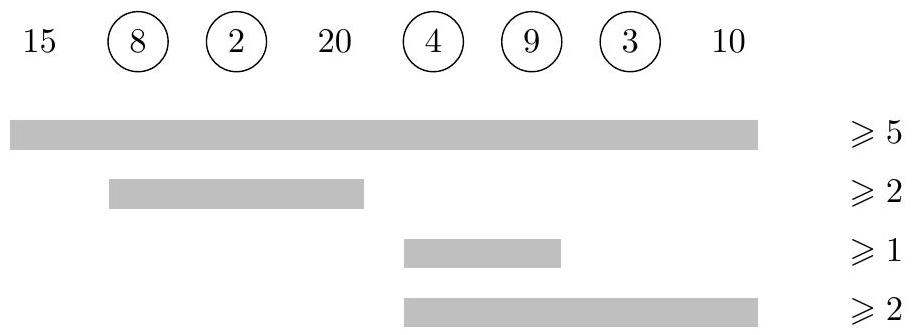
附加样例

1. $n=5$，$m=6$；简单测试点，答案为 $9$；
2. $n=20$，$m=5$；员工薪资要求为 $1$ 到 $20$ 的一个排列；
3. $n=1000$，$m=200$；满足 $c_{i}=((i-1) \bmod 10)+1$ $(1 \leq j \leq n)$ 以及 $s_{j}=5j-4$，$t_{j}=5j$，$p_{j}=1$ $(1 \leq j \leq m)$；
4. $n=200000$，$m=200000$；满足 $c_{i}=1$ $(1 \leq j \leq n)$以及 $s_{j}=1$，$t_{j}=j$，$p_{j}=\min(j, 50)$ $(1 \leq j \leq m)$。

数据范围与提示

详细子任务附加限制及分值如下表所示。

如果你的程序仅在第一行正确输出了最小成本，但提供的员工列表与该成本不符，则可获得该测试点 $50\%$ 的分数。