题目描述

题目译自 XXVII Olimpiada Informatyczna – Eliminacje do IOI Kompresja drzew binarnych

完全二叉树由一定数量的节点组成。每个节点有两个子节点，分别为左子节点和右子节点，或者没有任何子节点，这种情况下我们称之为叶子节点。如果节点 $v$ 是节点 $u$ 的子节点，则节点 $u$ 称为节点 $v$ 的父节点。树的根节点是唯一没有父节点的节点。在图示中，根节点通常绘制在树的顶部。例如，下图展示了一棵有 $15$ 个节点和 $8$ 个叶子节点的完全二叉树。

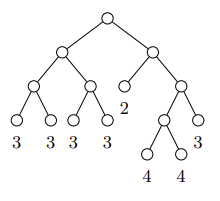
我们将二叉树的子树定义为任意一个节点及其所有后代节点（包括子节点、子节点的子节点等）。如果两棵子树没有公共节点，我们称它们为不相交的。节点的深度定义为从根节点到该节点的路径上节点数量，不包括根节点本身。因此，例如上图中的树，其叶子节点的深度依次为 $3, 3, 3, 3, 2, 4, 4, 3$。请注意，知道了叶子节点的深度序列，我们可以唯一地重建树的形状。

Bajtazar 是一名计算机科学家，专注于数据压缩。最近，他在研究使用前缀码的压缩方法，这种方法可以用完全二叉树来表示。如果使用某个前缀码进行压缩，描述该码的二叉树也必须包含在压缩文件中，因此树的描述应尽可能小。

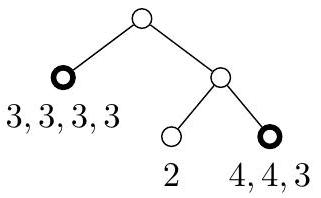
Bajtazar 提出了一种压缩完全二叉树的方法。他选择若干互不相交的子树，这些子树的叶子节点要么都在同一深度，要么在相差 $1$ 的两个深度上，然后将每棵子树替换为一个叶子节点。Bajtazar 以这种方式压缩树，使得结果树的节点数量尽可能少。例如，对上述树的压缩结果为一棵只有 $5$ 个节点的树：

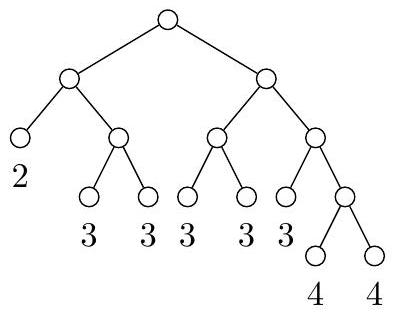
从前缀码的效率角度来看，二叉树的具体形状并不重要，重要的是叶子节点所在的深度。因此，我们说两棵树是等价的，如果它们的叶子深度多重集（即允许重复的集合）相同。例如，下图展示了一棵完全二叉树，其叶子深度与之前相同：

对其压缩后，得到一棵只有 $3$ 个节点的树：

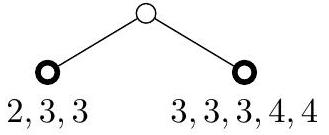
Bajtazar 拥有一棵描述某个前缀码的完全二叉树 $T$。他希望构建一棵与之等价的树 $T'$，使得对 $T'$ 进行压缩后得到的节点数量尽可能少。

输入格式

输入数据的第一行包含一个整数 $n$ $(1 \leq n)$，表示完全二叉树 $T$ 的叶子节点数量。

第二行包含 $n$ 个非负整数 $l_{1}, \ldots, l_{n}$，用单个空格分隔，表示该树中从左到右各叶子节点的深度。

输出格式

输出两行。

第一行应包含一个整数，表示从与树 $T$ 等价的某棵完全二叉树 $T'$ 压缩后得到的最小节点数量。

第二行应输出树 $T'$ 的叶子深度序列，从左到右排列。如果存在多个正确答案，你的程序可以输出其中任意一个。

8
3 3 3 3 2 4 4 3

3
2 3 3 3 3 3 4 4

附加样例

1. $n=10$；
2. $n=1024$，所有叶子节点均在深度 $10$；
3. $n=500000$，叶子深度为从 $1$ 到 $n-1$ 的连续数字，最后一个叶子节点的深度与倒数第二个相同，为 $n-1$。

数据范围与提示

详细子任务附加限制及分值如下表所示。

如果程序仅在第一行正确输出结果，但在第二行输出错误，则可获得该测试点 $50\%$ 的分数。但要求第二行输出的叶子深度必须是输入中的深度，顺序可以任意。