题目描述

题目译自 PA 2017 Runda 5 Giewont

著名的登山爱好者 Bajtazar 即将踏上一次新的探险之旅。这次，他被波兰塔特拉山的照片所吸引，决定征服吉沃特山的山峰。因此，他想知道自己需要攀登到多高的地方。然而，他在拜托西亚购买的塔特拉山地图质量很差，信息极不完整。

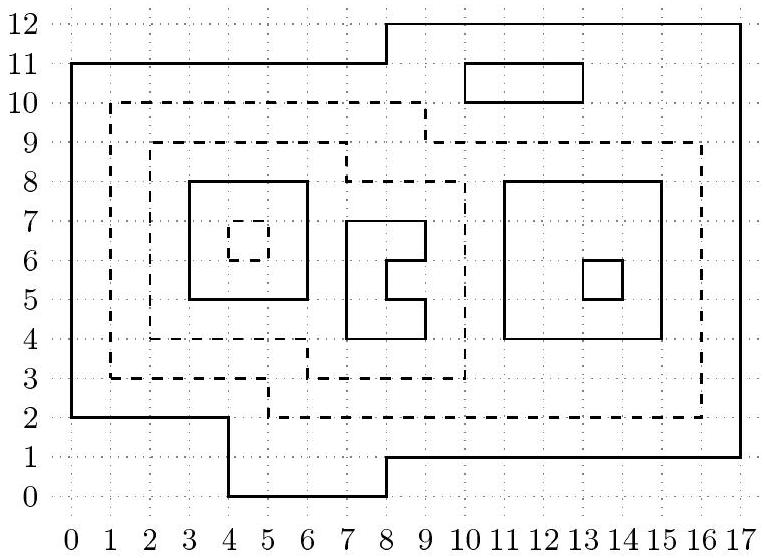
实际上，地图上唯一标注的内容就是等高线。我们可以在地图上引入一个矩形坐标系；每条等高线是一条闭合的普通折线，顶点坐标为整数，且边与坐标轴平行。等高线之间不交叉也不接触，但可以任意嵌套。我们假设存在一条“外部”等高线，它包含所有其他等高线。

Bajtazar 想从地图上读取最高山峰的高度，但等高线旁没有标注具体海拔高度。于是，他决定（名副其实地）从高处估算这个高度。由于地图上的山峰由一系列嵌套的等高线表示，每条等高线包含在上一条等高线内部，Bajtazar 认为这种嵌套序列越长，山峰可能就越高。

不幸的是，他怀疑地图上只包含了部分等高线，实际山峰可能更高。现在，他试图在地图上添加新的等高线，以获得尽可能高的山峰。请帮助 Bajtazar，编写一个程序完成这项任务。新添加的等高线必须是闭合的普通折线，满足与地图上等高线相同的条件（整数坐标、边与坐标轴平行、不与其他等高线交叉、包含在“外部”等高线内）。

输入格式

输入数据的第一行包含一个正整数 $n$，表示地图上的等高线数量。

接下来的 $n$ 行描述各条等高线。每行描述以一个偶数整数 $k$ 开头，表示该等高线的顶点数量。接着是 $k$ 个整数 $x_{1}, x_{2}, \ldots, x_{k}$ $(-10^{8} \leq x_{i} \leq 10^{8})$；等高线的顶点依次为 $(x_{1}, x_{2}), (x_{3}, x_{2}), (x_{3}, x_{4}), (x_{5}, x_{4}), \ldots, (x_{k-1}, x_{k}), (x_{1}, x_{k})$。

所有等高线的顶点总数不超过 $50000$。等高线以任意顺序给出。沿顶点顺序绕行任意等高线时，其“内部”始终位于左侧。

输出格式

输出应包含一个整数，表示通过添加新等高线可以获得的最 高山峰高度（即最长的嵌套等高线序列长度）。

6
4 3 5 6 8
8 7 4 9 5 8 6 9 7
4 13 5 14 6
10 8 1 17 12 8 11 0 2 4 0
4 11 4 15 8
4 10 10 13 11

5