题目描述

题目译自 PA 2016 Runda 5 Bilard Hilberta

在拜托西亚居民中，一种相当独特的游戏——希尔伯特台球——成为了最新的时尚潮流。游戏台的尺寸为 $2^{n+1} \times 2^{n+1}$，我们称 $n$ 为台面的大小。台面上放置了形成 $n$ 阶希尔伯特曲线的隔板。以下图片展示了 $n=1, 2, 3$ 的台面。

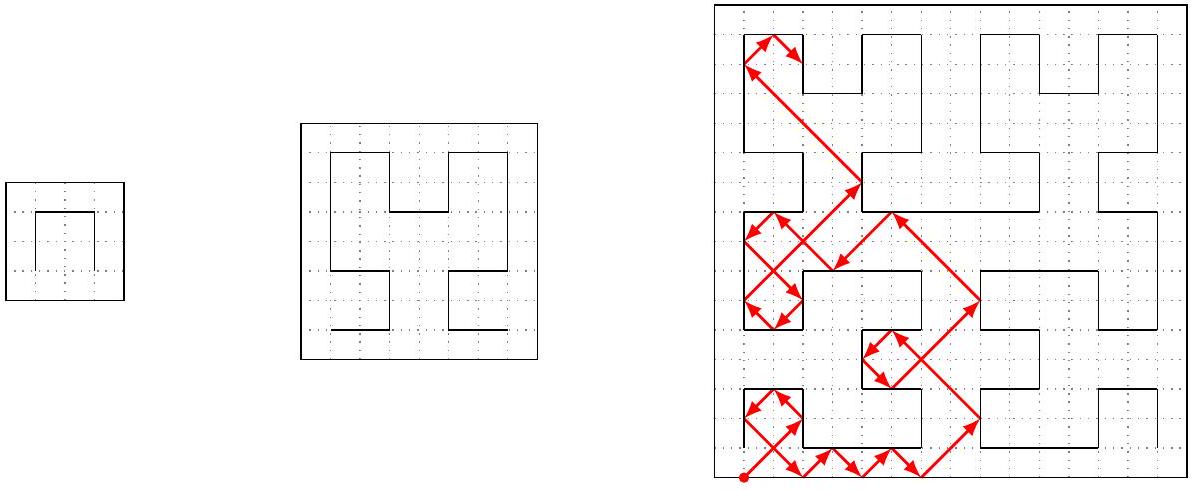
台面的左下角坐标为 $(0, 0)$，右下角坐标为 $(2^{n+1}, 0)$，右上角坐标为 $(2^{n+1}, 2^{n+1})$。1 阶希尔伯特曲线形成大小为 1 的台面隔板，如左图所示。对于 $n \geq 2$，大小为 $n$ 的台面隔板由四个 $n-1$ 阶希尔伯特曲线组成，分别位于台面的四个象限中，并由三条长度为 2 的连接隔板相连（参见图片）。左下角的曲线顺时针旋转 $90^{\circ}$，右下角的曲线逆时针旋转 $90^{\circ}$。

从坐标为 $(1, 0)$ 的点开始，以初始速度向量 $(1, 1)$ 发射一个台球，台球在运动过程中会与形成希尔伯特曲线的隔板以及台面边缘进行理想弹性碰撞。为简化问题，我们假设台球的大小可以忽略不计。需要计算台球在 $t$ 个时间单位后所在点的坐标。图中以红色标示了大小为 $n=3$ 的台面台球的初始路径；例如，在 $t=42$ 个时间单位后，台球将位于坐标为 $(3, 14)$ 的点。

输入格式

输入数据的第一行包含两个整数 $n$ 和 $z$ $(1 \leq n \leq 30, 1 \leq z \leq 100000)$，分别表示台面大小和查询数量。

接下来的 $z$ 行包含按升序排列的查询：第 $i$ 行包含一个整数 $t_{i}$ $(0 < t_{1} < t_{2} < \ldots < t_{z} < 2^{2(n+1)})$，表示第 $i$ 个查询的时间单位数。

输出格式

输出应包含恰好 $z$ 行，依次对应输入中的查询：第 $i$ 行应包含两个整数，用单个空格分隔，表示台球在 $t_{i}$ 个时间单位后所在的点的坐标。

3 2
1
42

2 1
3 14