题目描述
题目译自 Ukrainian Olympiads in Informatics 2024 Stage 4 Day1 T2. Подарунок Леді
在生日当天,莱蒂收到了一份礼物——一个网络。这个网络包含 n 个节点,编号为从 1 到 n 的整数。每个节点上写有一个字母,对于编号为 i 的节点,其字母记为 si。
某些节点之间存在单向连接。每个节点恰好有一个单向连接指向另一个节点。设从编号为 i 的节点出发的连接指向编号为 xi 的节点。注意,xi 可以等于 i,即从节点 i 出发的连接指向它自身。
定义 pi,0=i,且 pi,k=pxi,k−1。也就是说,pi,k 是将棋子放在编号为 i 的节点上,并沿连接移动 k 次后到达的节点编号。
莱蒂创建了一个 n×(3⋅n) 的矩阵 a,其中 ai,j=spi,j−1。也就是说,矩阵 a 的第 i 行是长度为 3⋅n 的字母序列,其第一个字母为 si,第二个字母为 sxi,第三个字母为 sxxi,依此类推……
莱蒂提供了矩阵 a 的某些行,并要求你构建一个符合这些已知行的网络。
输入格式
输入的第一行包含一个整数 n (1≤n≤2⋅103),表示网络中节点的数量。
接下来的 n 行描述矩阵 a。每行包含 3⋅n 个小写拉丁字母,表示矩阵 a 的对应行;或者包含一个字符 ?,表示莱蒂未提供该行信息。
保证至少存在一个符合条件的网络。
输出格式
输出第一行包含一个长度为 n 的小写拉丁字母字符串 s,表示网络节点上写着的字母。
输出第二行包含 n 个整数 x1,x2,…,xn (1≤xi≤n),表示从对应节点出发的连接指向的节点编号。
所构建的网络对应的矩阵必须在莱蒂提供的每一行上与矩阵 a 一致。
如果存在多个正确答案,可以输出任意一个。
4
abaaaaaaaaaa
baaaaaaaaaaa
aaaaaaaaaaaa
cccccccccccc
abac
2 3 3 4
在第一个样例中,x1=2 且 x2=3,因此 p1,0=1,p1,1=2,p1,2=3。由于 x3=3,对于 k≥3 的所有 p1,k 也等于 3。因此,第一个行的第二个字母为 s2,第三个字母为 s3。
以下是样例中的网络图示。节点角落中的数字表示节点编号,字母表示节点上写的值,箭头表示单向连接。
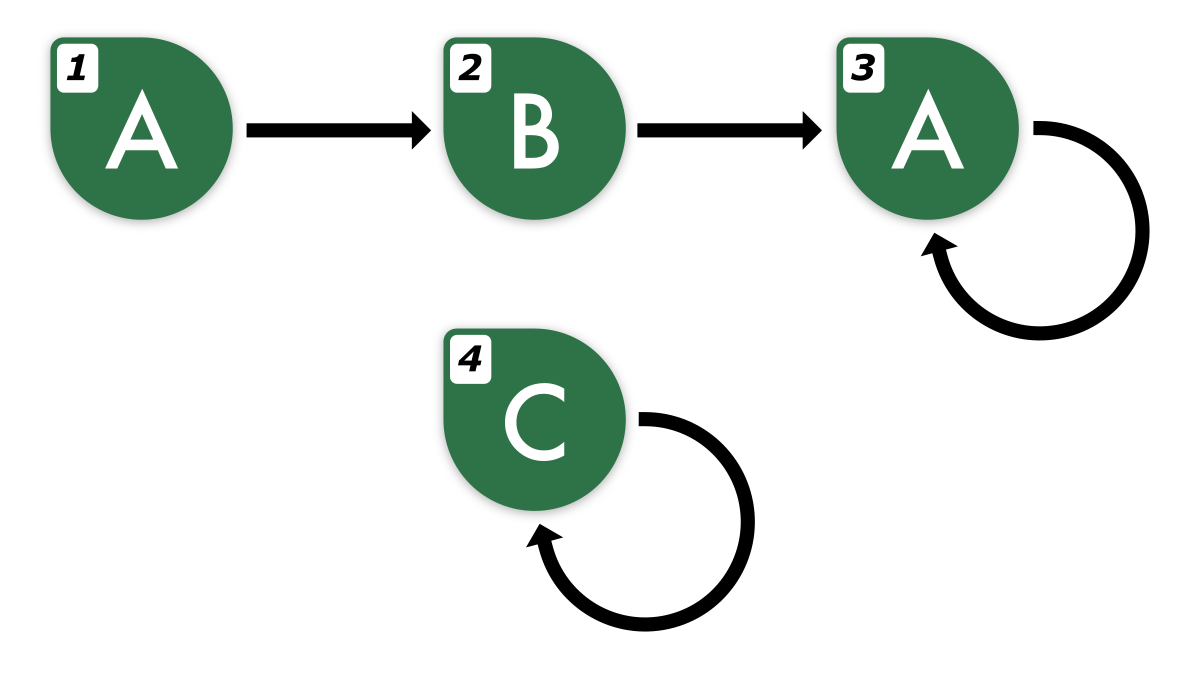
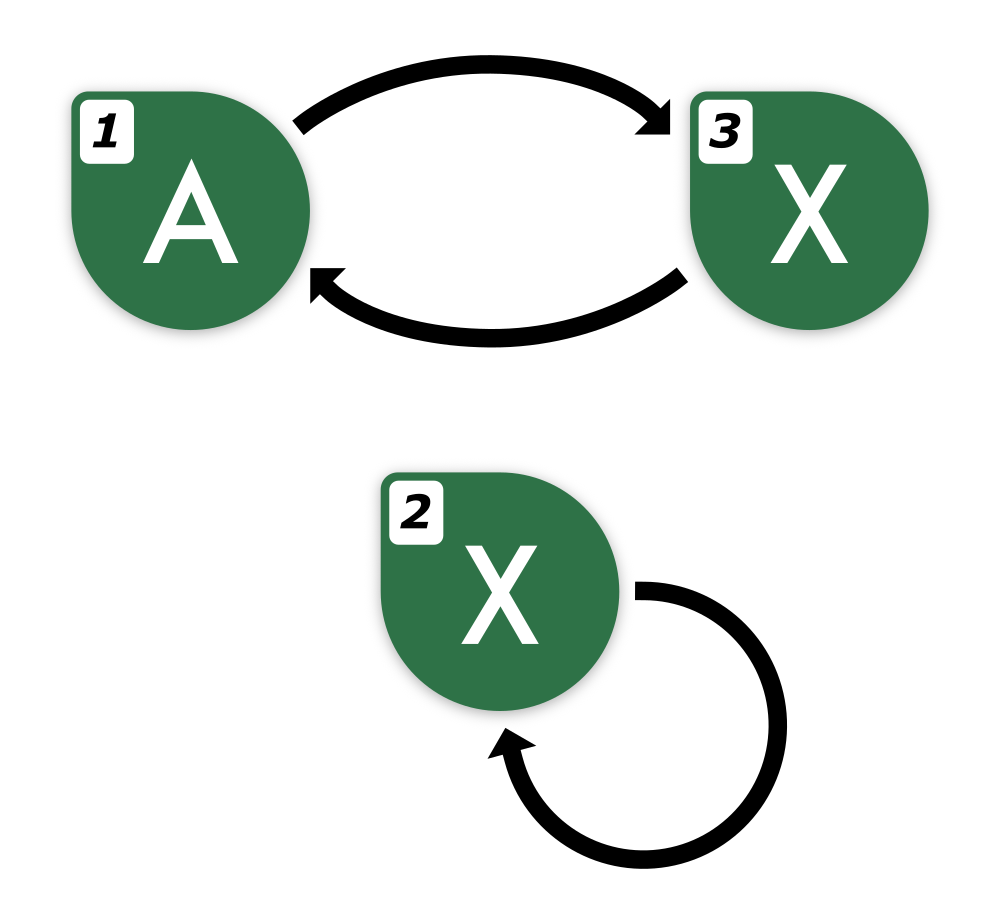
3
axaxaxaxa
xxxxxxxxx
?
axx
3 2 1
数据范围与提示
设 q 为莱蒂未提供的行数。
定义网络为成对和单节点集合,如果网络可以分解为一些节点(其中 xv=v,即连接指向自身)和一些节点对 (a,b)(其中 xa=b 且 xb=a)。
定义网络为星形集合,如果网络可以分解为若干「星形」,每个星形包含一个中心节点 v(其中 xv=v,即连接指向自身)和一组次级节点 y={y1,y2,…,yk}(其中对于 1≤i≤k,有 xyi=v)。注意,星形的规模可以不同,也可以仅包含一个中心节点。
定义网络为以节点 v 为根的树,如果节点 v 的连接指向自身(即 xv=v),且对于其他所有节点,可以通过网络连接到达节点 v(即对于每个 1≤i≤n,存在 k 使得 pi,k=v)。
定义网络为循环,如果从任意节点出发,可以通过网络连接到达任意其他节点(即对于所有 1≤i,j≤n,存在 k 使得 pi,k=j)。
详细子任务附加限制及分值如下表所示:
| 子任务 |
分值 |
附加限制 |
| 1 |
10 |
n≤5, q=0 |
| 2 |
6 |
n≤300, q=0, xxi=i(对于 1≤i≤n,网络为成对和单节点集合) |
| 3 |
6 |
n≤300, q=0, xxi=xi(对于 1≤i≤n,网络为星形集合) |
| 4 |
9 |
n≤300, q=0, x1=1 且 xi<i(对于 2≤i≤n,网络为以节点 1 为根的树) |
| 5 |
9 |
n≤300, q=0, 对于所有 1≤i,j≤n 存在 k 使得 pi,k=j(网络为循环) |
| 6 |
13 |
n≤300, q=0 |
| 7 |
25 |
n≤300 |
| 8 |
10 |
n≤2⋅103, q=0 |
| 9 |
12 |
无附加限制 |

