题目描述

题目译自 Ukrainian Olympiads in Informatics 2020 Stage 4 Day1 T2. Шахове поле

安娜小姐最近参加了一家IT公司的面试。在面试中，她得到了一道非常有趣的题目：

给定一个被划分为单位正方形的平面，每个正方形的边长为 $1$。每个正方形被涂成白色或黑色。

如果一个平面由高度为 $n$ 个单位、宽度为 $m$ 个单位的矩形组成，并且这些矩形都被涂成白色或黑色，同时每个白色矩形仅与黑色矩形相邻，反之每个黑色矩形仅与白色矩形相邻，我们称这个平面为具有参数 $n$ 和 $m$ 的棋盘平面。

例如，下图展示了一个具有参数 $2$ 和 $3$ 的棋盘平面（坐标轴用蓝色表示）：

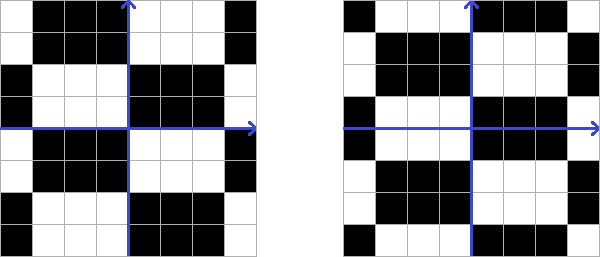
而以下平面则不是：

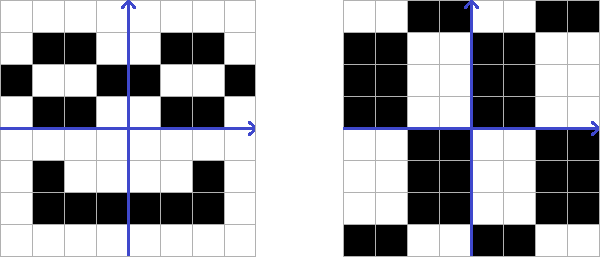
正如你可能已经注意到的，具有参数 $n$ 和 $m$ 的棋盘平面往往有许多种。任务是计算有多少种这样的平面。但这太简单了。

安娜还被告知了平面上的 $k$ 个正方形及其颜色。她需要找出具有参数 $n$ 和 $m$ 的棋盘平面的数量，使得这些指定坐标的正方形具有给定的颜色。请帮助她完成这个任务！

更形式化地，给你 $k$ 个三元组数字：$x_i, y_i, c_i$，其中 $(x_i, y_i)$ 是正方形左下角的坐标，$c_i$ 为 $0$ 表示该正方形应涂成黑色，为 $1$ 表示应涂成白色。你需要输出具有参数 $n$ 和 $m$ 的不同棋盘平面的数量，这些平面满足给定的限制条件。两个棋盘平面被认为是不同的，如果存在至少一个正方形在这两个平面上的颜色不同。

输入格式

第一行包含四个整数 $n, m, k, g$ $(1 \leq k \leq 10^{5}, 1 \leq n, m \leq 10^{9}, 0 \leq g \leq 4)$，分别表示每个矩形的高度、宽度、已知点的数量以及子任务编号。

接下来的 $k$ 行，每行包含三个整数 $x_i, y_i, c_i$ $(1 \leq x_i, y_i \leq 10^{9}, 0 \leq c_i \leq 1)$，分别表示正方形的坐标和颜色。请注意，点的坐标可能会重复。

输出格式

输出一个整数，表示具有参数 $n$ 和 $m$ 且满足给定限制条件的不同棋盘平面的数量。

2 2 4 0
1 4 0
2 3 0
3 3 1
4 4 1

1

2 6 2 0
1 2 0
3 2 0

8

样例解释

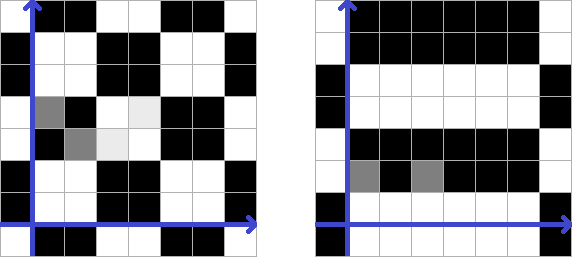
在第一个样例中，左图显示了唯一符合限制条件的平面。

在第二个样例中，右图显示了满足条件的 $8$ 种可能平面中的一种。

数据范围与提示

详细子任务附加限制及分值如下表所示：