题目描述

译自 NOISG 2024 Final T5. Field

蜗牛斯图尔特生活在一片田野上。田野可描述为一个无限平面（二维空间）。田野上每个整数坐标点上都有可食用的植物。斯图尔特的家位于原点 $(0,0)$。

正在下雨，斯图尔特能够轻松移动。每小时，他可以选择当前位置旁边的四个可食用植物之一，移动到那里并吃点东西。形式上，若他位于坐标 $(x, y)$，他可以移动到 $(x+1, y), (x, y+1), (x-1, y)$ 或 $(x, y-1)$。只要雨继续下，他可以继续旅行，但也可以随时选择在任何可食用植物的位置停下来，包括直接留在家里。

然而，田野上有 $n$ 个深水坑。每个水坑覆盖一个矩形区域，水太深，斯图尔特无法安全通过。第 $i$ 个水坑阻止斯图尔特移动到满足 $a[i] \leq x \leq b[i]$ 且 $c[i] \leq y \leq d[i]$ 的任何整数坐标 $(x, y)$。水坑可能重叠。

雨会持续多久尚不清楚。回答 $q$ 个由 $t$ 定义的相同类型查询：

• 若 $t=1$，斯图尔特希望访问坐标 $(x[j], y[j])$ 处的植物。假设雨永不下停，求他到达 $(x[j], y[j])$ 所需的最短时间（以小时为单位）。若无法到达目标，输出 $-1$。
• 若 $t=2$，假设雨将持续 $m[j]$ 小时。计算斯图尔特在最多 $m[j]$ 小时内可以结束旅行的不同位置数量。

输入格式

程序需从标准输入读取数据。

输入的第一行包含三个整数 $n, t, q$，分别表示水坑数量、查询类型和查询数量。

接下来的 $n$ 行，每行包含四个整数 $a[i], b[i], c[i], d[i]$，描述一个水坑。

若 $t=1$，接下来的 $q$ 行，每行包含两个整数 $x[j], y[j]$，描述一个目标位置。

否则，若 $t=2$，接下来的 $q$ 行，每行包含一个整数 $m[j]$，描述一次查询的雨持续时间。

输出格式

程序需向标准输出输出结果。

对于 $q$ 个查询中的每一个，在新行输出一个整数，表示答案。

5 1 4
-4 -3 -2 5
-6 4 4 4
1 2 0 6
4 4 -1 4
-2 6 -4 -2
-1 2
3 3
0 6
2 -3

3
8
-1
-1

下页的图表描述了原点周围的区域。蓝色矩形表示无法进入或通过的水坑。

无法在不进入水坑的情况下到达最后两个目标位置。注意，最后一个目标位置被水坑覆盖。

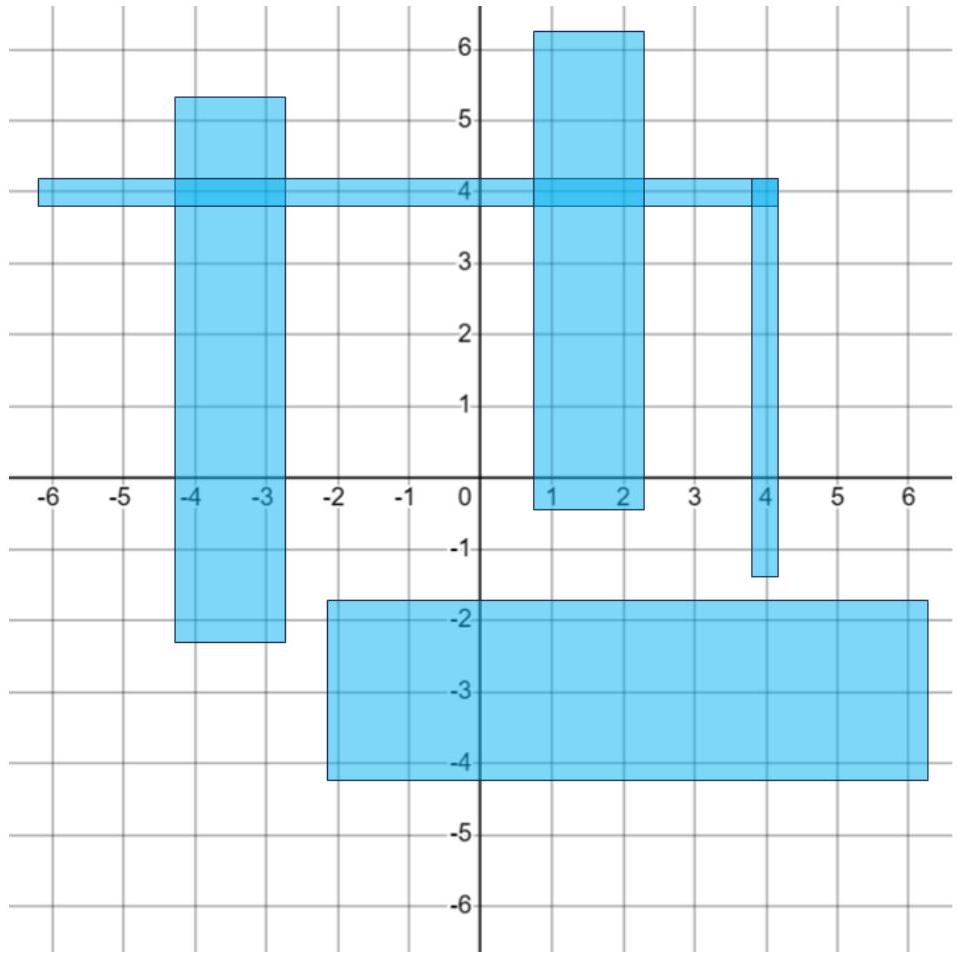
这个样例满足子任务 $1, 3$ 的限制。

2 1 4
-1000000000 -1 0 999999999
0 999999999 -1000000000 -1
1 1
-1 1
-1 -1
1 -1

2
-1
4000000002
-1

这个样例满足子任务 $2, 3$ 的限制。

2 2 6
-2 5 1 1
0 1 -3 -2
1
2
3
4
5
6

4
8
13
21
32
48

这个样例满足子任务 $4, 6, 7, 8, 9$ 的限制。

2 2 4
0 9999999 -10000000 -1
-10000000 -1 10000000 29999999
12
1234
123456
12345678

235
2285986
22862261089
231374765559370

这个样例满足子任务 $5, 6, 7, 8, 9$ 的限制。

数据范围与提示

对于所有输入数据，满足：

• $1 \leq n \leq 400$
• $1 \leq t \leq 2$
• $1 \leq q \leq 200000$
• $-10^{9} \leq a[i] \leq b[i] \leq 10^{9}$
• $-10^{9} \leq c[i] \leq d[i] \leq 10^{9}$
• $(0,0)$ 不被任何水坑覆盖。
• 若 $t=1$，则 $-10^{9} \leq x[j], y[j] \leq 10^{9}$
• 若 $t=2$，则 $1 \leq m[j] \leq 10^{9}$

详细子任务附加限制及分值如下表所示：