题目描述

译自 NOISG 2025 Final T3. Reachability

羊之国是一个拥有 $n$ 个城市的国家。有 $n-1$ 条道路连接不同的城市对。第 $j$ 条道路直接连接城市 $u[j]$ 和 $v[j]$。初始时，通过这些道路可以从任意城市到达其他任意城市。

羊之国的所有 $n-1$ 条道路计划进行翻新。根据翻新计划，每条道路 $j$ 将处于以下四种状态之一：

1. 双向：城市 $u[j]$ 和 $v[j]$ 的居民均可通过此道路进入对方城市。
2. 从城市 $u[j]$ 到 $v[j]$ 的单向：仅城市 $u[j]$ 的居民可通过此道路进入城市 $v[j]$。
3. 从城市 $v[j]$ 到 $u[j]$ 的单向：仅城市 $v[j]$ 的居民可通过此道路进入城市 $u[j]$。
4. 关闭：城市 $u[j]$ 和 $v[j]$ 的居民均不可通过此道路进入对方城市。

不幸的是，翻新计划丢失了！

为了恢复计划，你询问了每个城市的市长，在翻新计划下从他们的城市可以到达的城市数量。第 $i$ 位市长回复了 $l[i]$。然而，部分市长可能提供了错误的数据。

如果存在一个序列 $c_{1}, c_{2}, c_{3}, \ldots, c_{k}$，其中 $c_{1}=u$，$c_{k}=v$，且对于所有 $1 \leq x \leq k-1$，从 $c_{x}$ 到 $c_{x+1}$ 存在可通行的道路，则城市 $v$ 可从城市 $u$ 到达。特别地，每个城市都可以到达自身。

请帮助羊之国判断是否存在一个与所有市长报告的可达城市数量一致的翻新计划！

输入格式

程序需从标准输入读取数据。

输入的第一行包含一个整数 $n$。

第二行包含 $n$ 个空格分隔的整数 $l[1], l[2], \ldots, l[n]$。

接下来的 $n-1$ 行，每行包含两个空格分隔的整数，第 $j$ 行表示 $u[j]$ 和 $v[j]$。

输出格式

程序需向标准输出输出结果。

如果存在与所有市长报告的可达城市数量一致的翻新计划，输出 YES；否则输出 NO。

9
5 2 3 5 2 3 1 1 1
1 4
4 5
2 5
3 6
5 6
6 9
7 8
4 7

YES

请参考下方的图示。翻新计划与所有市长报告的可达城市数量一致。

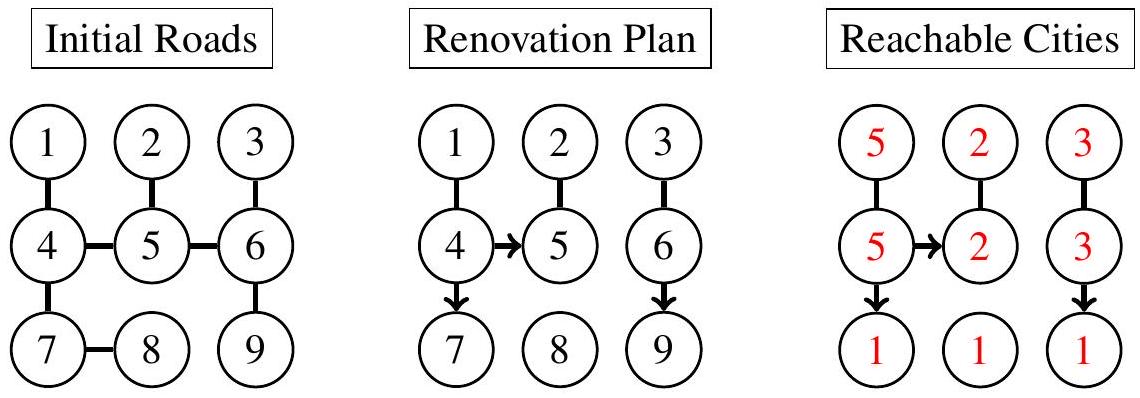
这个样例满足子任务 $2,5,6$ 的限制。

9
5 2 3 5 2 3 1 1 2
1 4
4 5
2 5
3 6
5 6
6 9
7 8
4 7

NO

不存在与所有市长报告的可达城市数量一致的翻新计划。

这个样例满足子任务 $2,4,5,6$ 的限制。

7
3 3 1 3 2 1 2
3 4
1 2
6 2
7 3
5 6
4 2

YES

这个样例满足子任务 $1,2,5,6$ 的限制。

数据范围与提示

对于所有输入数据，满足：

• $1 \leq n \leq 5000$
• $1 \leq l[i] \leq n$，对于所有 $1 \leq i \leq n$
• $1 \leq u[j], v[j] \leq n$，对于所有 $1 \leq j \leq n-1$
• 对于所有 $1 \leq j \leq n-1$，$u[j] \neq v[j]$
• 初始时，通过道路可从任意城市到达其他任意城市。

详细子任务附加限制及分值如下表所示：