题目描述
译自 NOISG 2025 Final T4. Robots
欢乐国被建模为一个 (h+2)×(w+2) 的网格。网格的行从上到下编号为 0 到 h+1,列从左到右编号为 0 到 w+1。位于行 r 和列 c 的格子称为格子 (r,c)。
初始时,网格中的所有格子为白色,除了最右列的所有格子为黑色。
列 1 到 w 每列恰好包含一个特殊格子。这些特殊格子将被涂成红色或蓝色。网格的边缘(即最上行、最下行、最左列和最右列)永远不包含特殊格子。
若干机器人将被放置在最左列的格子上,并根据所在格子的颜色移动:
- 若格子为白色,机器人向右移动。
- 若格子为红色,机器人向上移动。
- 若格子为蓝色,机器人向下移动。
- 若格子为黑色,机器人停止移动。
机器人之间不会发生碰撞;每个机器人独立移动。多个机器人可以占据同一个格子。
一个查询包含两个整数 a 和 b (1≤a<b≤h)。对于每个 a≤c≤b,将有一个机器人从格子 (c,0) 开始移动。在所有可能的特殊格子涂成红色或蓝色的配置下,确定机器人最终占据的不同格子的最小数量。
注意,不同查询可能对应不同的特殊格子颜色配置。
输入格式
程序需从标准输入读取数据。
输入的第一行包含两个空格分隔的整数 h 和 w。
第二行包含 w 个空格分隔的整数 x[1],x[2],…,x[w],表示特殊格子为 (x[1],1),(x[2],2),…,(x[w],w)。
第三行包含一个整数 q。
接下来的 q 行,每行包含两个空格分隔的整数,第 i 行表示 a[i] 和 b[i]。
输出格式
程序需向标准输出输出结果。
输出包含 q 行,第 i 行包含一个整数,表示第 i 个查询的答案。
4 4
3 2 4 1
3
1 4
1 3
2 4
2
1
1
网格的颜色配置如下,特殊格子以紫色表示。
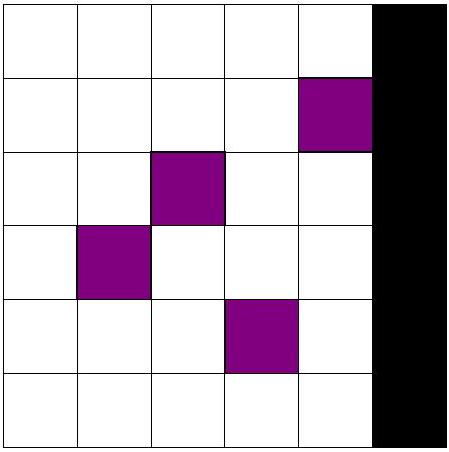
对于第一个查询,可以将特殊格子 (3,1) 和 (4,3) 涂成蓝色,(2,2) 和 (1,4) 涂成红色,得到以下结果:
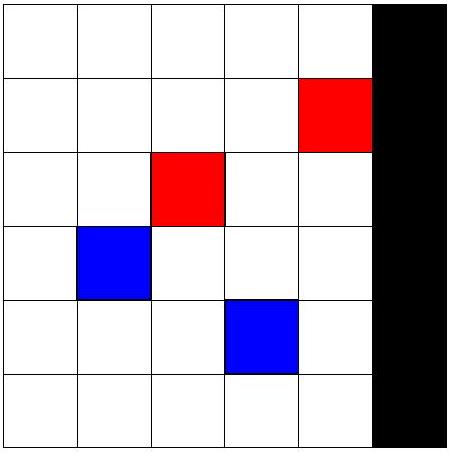
- 从 (1,0) 开始的机器人移动到 (1,1),(1,2),(1,3),(1,4),(0,4),(0,5),最终停在 (0,5)。
- 从 (2,0) 开始的机器人移动到 (2,1),(2,2),(1,2),(1,3),(1,4),(0,4),(0,5),最终停在 (0,5)。
- 从 (3,0) 开始的机器人移动到 (3,1),(4,1),(4,2),(4,3),(5,3),(5,4),最终停在 (5,5)。
- 从 (4,0) 开始的机器人移动到 (4,1),(4,2),(4,3),(5,3),(5,4),最终停在 (5,5)。
机器人最终停在 2 个不同格子 (0,5) 和 (5,5),因此输出 2。
对于第二个查询,可以按以下方式涂色特殊格子:
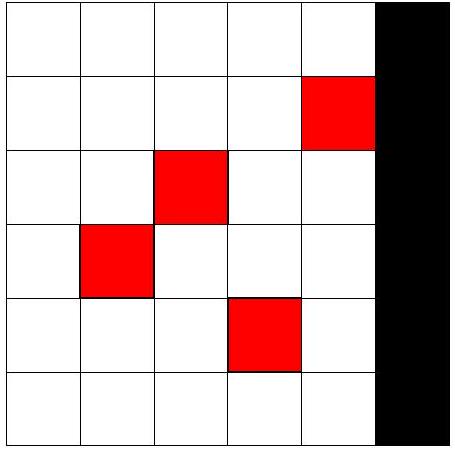
从 (1,0),(2,0),(3,0) 开始的机器人最终都停在 (0,5)。
对于第三个查询,可以按以下方式涂色特殊格子:
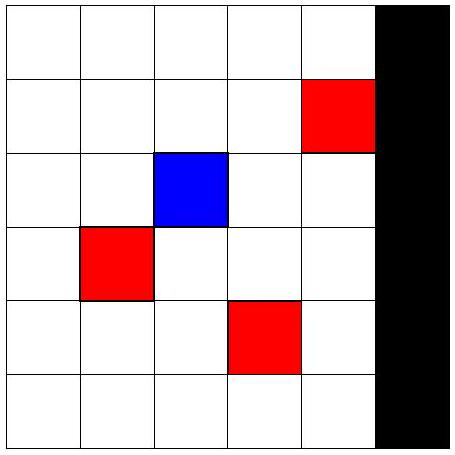
从 (2,0),(3,0),(4,0) 开始的机器人最终都停在 (3,5)。
这个样例满足子任务 1,4,5 的限制。
15 16
5 15 3 4 13 8 3 7 14 6 2 10 11 12 9 1
20
4 10
7 15
5 15
2 6
7 15
5 15
12 15
13 14
5 14
13 14
2 11
3 11
2 5
9 11
3 15
5 14
1 13
3 7
7 12
4 8
2
2
3
2
2
3
1
1
3
1
3
2
1
1
3
3
4
1
2
1
这个样例满足子任务 1,4,5 的限制。
数据范围与提示
对于所有输入数据,满足:
- 1≤w,q≤200000
- 2≤h≤200000
- 1≤x[j]≤h,对于所有 1≤j≤w
- 1≤a[i]<b[i]≤h,对于所有 1≤i≤q
详细子任务附加限制及分值如下表所示:
| 子任务 |
分值 |
附加限制 |
| 1 |
10 |
h,w≤16,q≤20 |
| 2 |
4 |
a[i]+1=b[i] |
| 3 |
12 |
x[1]<x[2]<⋯<x[w] |
| 4 |
43 |
h,w,q≤5000 |
| 5 |
31 |
无附加限制 |



