题目描述

题目译自 Ukrainian Olympiads in Informatics 2019 Stage 4 Day2 T1. Труби

科扎克·武斯想要成为波托科兰迪亚的总统，而要做到这一点，按照惯例，他需要为善良的公民做一些好事，让他们变得更加友善，同时也让科扎克·武斯在人民中更加受欢迎。因此，他决定修复国家的自来水系统。该系统位于地下，为了简化问题，它被划分为大小相同的正方形片段，形成一个 $n \times m$ 的网格。片段从上到下编号为 $1$ 到 $n$，从左到右编号为 $1$ 到 $m$。每个片段可能是空的（用符号 $0$ 表示），也可能包含一种类型的管道，共 $6$ 种类型：

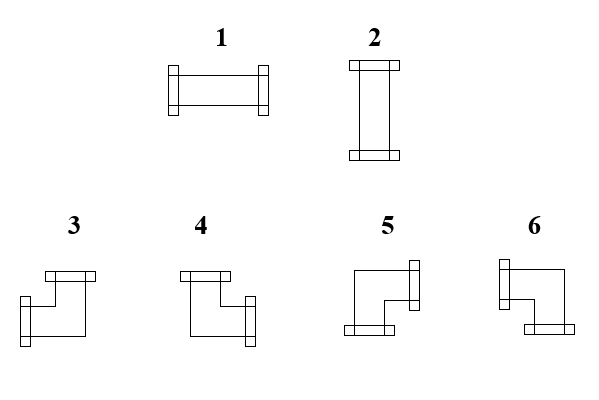
如果每条管道的每个端口都与其他管道的端口相连，我们称该自来水系统为闭合的。

最近，你被任命为科扎克·武斯在自来水事务方面的副手，因此现在你可以将任何管道旋转一个以 $90^{\circ}$ 为倍数的角度。你的任务是，通过旋转管道使自来水系统成为闭合的，或者确定这是不可能的。

输入格式

第一行包含三个整数 $n, m, g$ $(1 \leq n, m \leq 400, 0 \leq g \leq 8)$，分别表示网格的长度、宽度和子任务编号。

接下来的 $n$ 行，每行包含 $m$ 个整数 $a_{i,1}, a_{i,2}, \ldots, a_{i,m}$ $(0 \leq a_{i,j} \leq 6)$，表示坐标为 $(i, j)$ 的网格单元中管道的类型。

输出格式

如果无法通过旋转管道形成闭合系统，则输出 NO。

否则，输出 YES，并在接下来的 $n$ 行中每行输出 $m$ 个整数，描述通过旋转形成的闭合系统，格式如上所述。

5 5 0
0 0 0 0 0
0 3 1 2 4
0 2 0 0 1
0 1 0 0 1
0 6 2 2 5

YES
0 0 0 0 0
0 5 1 1 6
0 2 0 0 2
0 2 0 0 2
0 4 1 1 3

样例的说明图示：初始状态和闭合状态（如果存在）：

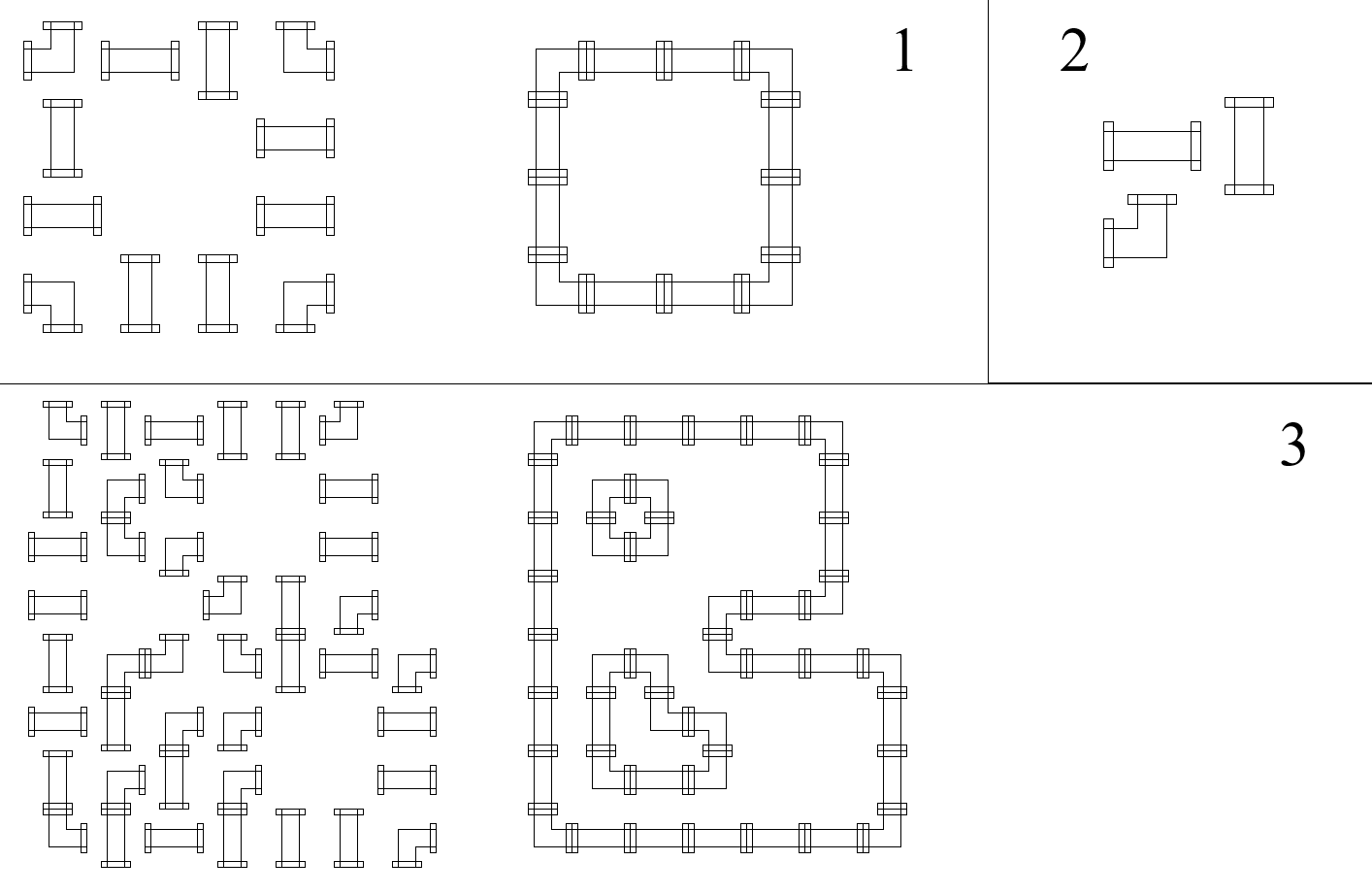
数据范围与提示

详细子任务附加限制及分值如下表所示：