题目描述

题目译自 European Girls' Olympiad in Informatics 2025 Day1 T1. Gift Boxes

今年的 EGOI 在波恩举办。组织者希望为比赛中的每个团队分发最多一个礼品盒，每个团队由编号 $0$ 到 $T-1$ 表示。参赛者站在一排，但他们混杂在一起，同一团队的人可能并不站在一起。请注意，队列中至少有一个团队有超过一个人。队列中共有 $N$ 个人。第 $i$ 个人属于团队 $a_{i}$。问题在于：每个团队最多只能收到一个礼品盒。为了确保分发过程顺利进行——并愿意因此让一些团队没有礼品——组织者希望在分发礼品时只暂停一次，跳过一些参赛者后再继续分发礼品盒。换句话说，他们将跳过一段连续的参赛者区间 $[\ell, r]$。

并非每个团队都需要收到礼品。尽管如此，组织者希望在确保没有团队收到两个或更多礼品的前提下，最大化收到礼品的团队数量，这等同于在此条件下最小化被跳过的参赛者数量。请帮助组织者决定何时暂停以及何时继续分发礼品，使得被跳过的参赛者尽可能少。

输入格式

第一行输入包含两个整数 $T$ 和 $N$，分别表示团队数量和队列中的参赛者数量。

第二行包含 $N$ 个整数 $a_{i}$，其中第 $i$ 个整数表示队列中位置 $i$ 的人所属的团队。保证每个从 $0$ 到 $T-1$ 的整数至少出现一次。

输出格式

输出两个整数 $\ell$ 和 $r$，其中 $\ell$ 是被跳过的第一个人的编号，$r$ 是被跳过的最后一个人的编号。注意，$\ell$ 和 $r$ 的编号范围是从 $0$ 到 $N-1$。如果有多个解，输出任意一个即可。

4 5
1 3 0 2 3

1 1

有两种可能的输出：$1 1$ 对应实心蓝色线，$4 4$ 对应红色虚线，如下图所示。无论哪种方式，四个团队都收到礼品，且没有团队收到超过一个礼品。

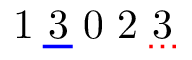
第一个样例满足子任务 $1, 3, 5, 6$ 的限制条件。

3 6
1 0 2 2 1 0

0 2

同样，有两种可能的输出：$0 2$ 和 $3 5$，如下图所示。在两种情况下，三个团队都收到礼品。

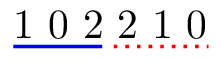
第二个样例满足子任务 $2, 3, 4, 5, 6$ 的限制条件。

4 8
0 2 0 1 2 1 3 3

2 6

最优解是三个团队收到礼品，如下所示。编号为 $0, 1, 7$ 的参赛者分别属于团队 $0, 2, 3$，他们收到礼品。这是唯一可能的解。

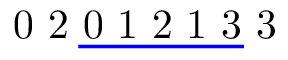
第三个样例满足子任务 $3, 4, 5, 6$ 的限制条件。

3 6
1 1 2 0 1 0

0 3

第四个样例满足子任务 $3, 5, 6$ 的限制条件。同样有两种可能的输出：0 3 和 1 4，如下图所示。在两种情况下，只有两个团队（团队 $0$ 和团队 $1$）收到礼品。团队 $2$ 没有收到礼品，因为如果给团队 $2$ 礼品，就必须给团队 $0$ 或 $1$ 两个礼品，这是严格禁止的。

4 6
0 1 2 0 3 2

2 3

唯一可能的答案是 $2 3$，如下图所示。四个团队都收到礼品。

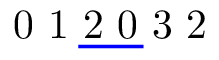
第五个样例满足子任务 $3, 5, 6$ 的限制条件。

5 13
3 3 3 1 2 0 3 3 2 1 4 1 0

1 9

最多有四个团队（共五个团队）可以收到礼品，如下所示。编号为 $0, 10, 11, 12$ 的参赛者分别属于团队 $3, 4, 1, 0$，他们收到礼品。这是唯一可能的解。

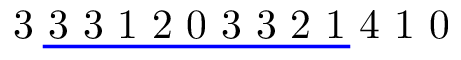
第六个样例满足子任务 $3, 5, 6$ 的限制条件。

数据范围与提示

对于所有输入数据，满足：

• $1 \leq T < N \leq 500000$。
• $0 \leq a_{i} \leq T-1$。

详细子任务附加限制及分值如下表所示。