题目描述

题目译自 European Girls' Olympiad in Informatics 2025 Day2 T1. A String Problem

Lara 非常喜欢跳蚤市场。上周六，波恩举办了德国最大的跳蚤市场之一——Rheinaue-Flohmarkt。当然，Lara 整天都在那里，漫步市场、讨价还价，买了各种稀奇古怪的东西。她带回家最有趣的东西是一个完美圆形的小竖琴。当她想开始弹奏时，她注意到琴弦杂乱无章，而不是彼此平行。

具体来说，圆形框架上均匀分布着 $2 \cdot N$ 个销钉。$N$ 根琴弦中的每一根都由两个销钉固定，每个销钉恰好连接一根琴弦。

Lara 对竖琴了解不多，但她强烈怀疑琴弦应该对齐成彼此平行的样子。为了解决这个问题，她决定重新安装琴弦。每一步，她可以将一根琴弦的一端从其销钉上取下，并重新连接到另一个销钉上。在这个过程中，多个琴弦的端点可以连接到同一个销钉上。最后，每个销钉上应该再次恰好连接一根琴弦，并且 $N$ 根琴弦应该彼此平行。

下面你可以看到两个带有平行琴弦的竖琴示例。

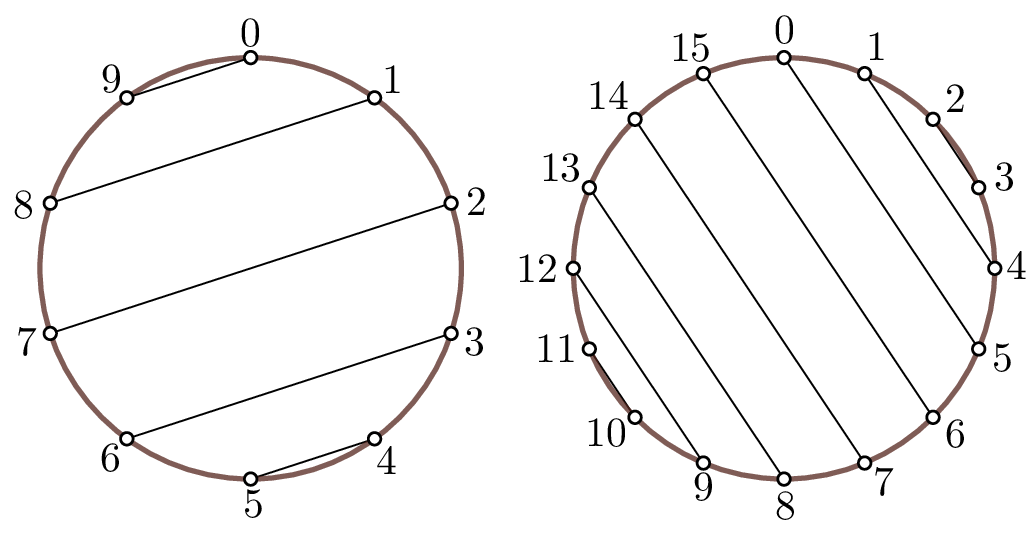
由于每次重新安装琴弦都需要很多工作，Lara 希望以尽可能少的步骤重新安装竖琴。帮助 Lara 找到一个最少步骤的重新安装序列！

输入格式

输入的第一行包含一个整数 $N$，表示琴弦的数量。琴弦编号为 $0$ 到 $N-1$。

接下来有 $N$ 行，其中第 $i$ $(0 \leq i \leq N-1)$ 行包含两个整数 $a_{i}$ 和 $b_{i}$，表示固定第 $i$ 根琴弦的两个销钉。销钉按顺时针顺序编号为 $0$ 到 $2 \cdot N-1$。每个销钉恰好连接一根琴弦。

输出格式

输出一个整数 $K$，表示重新安装竖琴使得所有琴弦彼此平行所需的最小步骤数。

接下来输出 $K$ 行，每行包含三个整数 $p, s, e$ $(0 \leq p \leq N-1, 0 \leq s, e \leq 2 \cdot N-1)$，表示在解决方案的这一步中，应将第 $p$ 根琴弦的一端从销钉 $s$ 上取下，并重新连接到销钉 $e$ 上。

注意，如果在那一刻第 $p$ 根琴弦未连接到销钉 $s$，则移动序列被认为是错误的。

如果存在多个答案，你可以输出其中任意一个。注意，部分正确的答案仍可能获得一些分数，如下一节所述。

5
1 5
4 9
6 3
2 7
0 8

3
4 8 9
0 5 8
1 9 5

在第一个样例中，我们有一个有 $5$ 根琴弦的竖琴。在第一步中，琴弦 $4$ 从销钉 $8$ 取下并重新连接到销钉 $9$。在下一步中，琴弦 $0$ 从销钉 $5$ 取下并重新连接到销钉 $8$。在最后一步中，琴弦 $1$ 从销钉 $9$ 取下并重新连接到销钉 $5$。现在，每个销钉上恰好连接一根琴弦，并且所有琴弦彼此平行。此序列如下图所示。

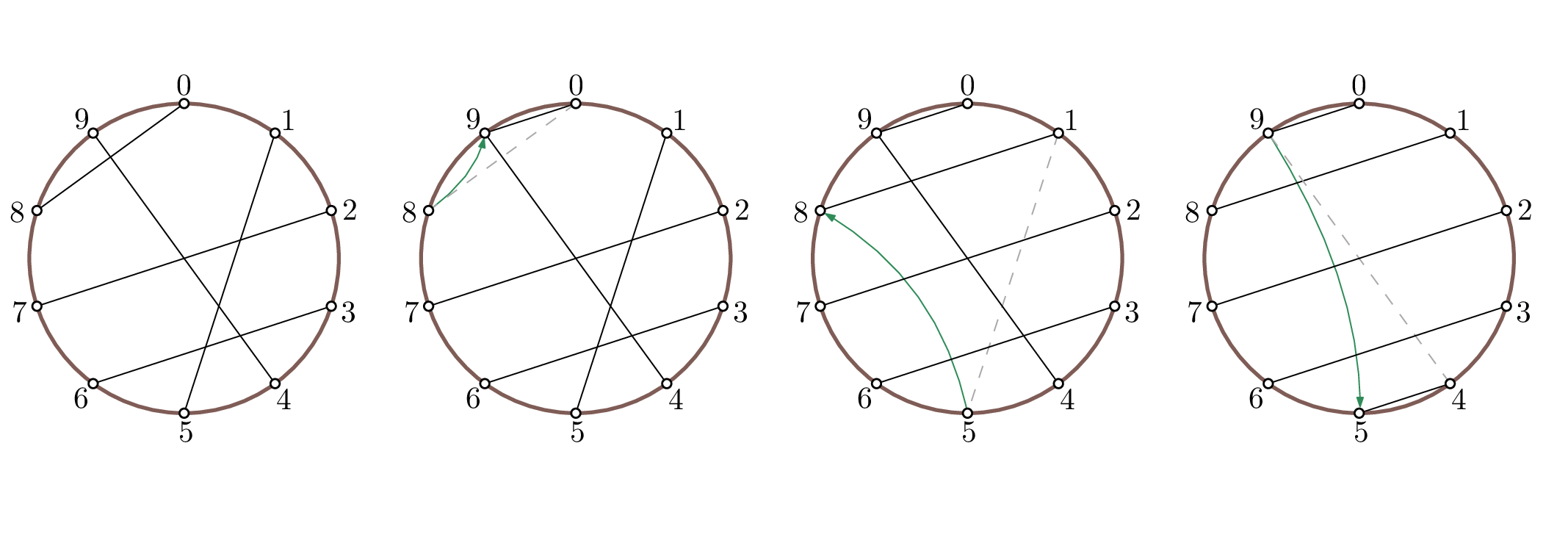
第一个样例满足子任务 $4, 5$ 的限制条件。

5
0 1
3 2
4 5
6 7
9 8

4
1 3 9
4 9 3
2 5 7
3 7 5

下图显示了样例 $2,3,4$ 的竖琴初始状态。

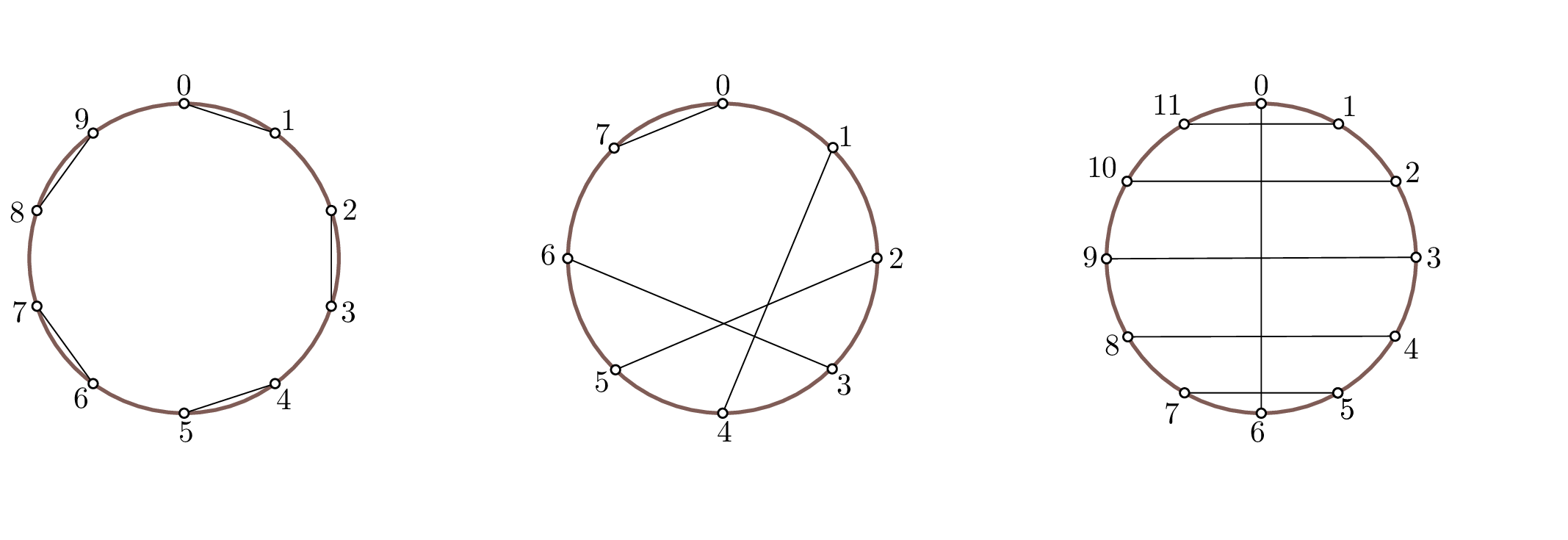
第二个样例满足子任务 $1, 3, 4, 5$ 的限制条件。

4
1 4
6 3
5 2
7 0

2
0 4 6
1 6 4

第三个样例满足子任务 $2, 4, 5$ 的限制条件。

6
3 9
7 5
10 2
0 6
1 11
8 4

6
3 6 1
4 1 2
2 2 3
0 3 4
5 4 5
1 5 6

第四个样例满足子任务 $3, 4, 5$ 的限制条件。

数据范围与提示

对于所有输入数据，满足：

• $4 \leq N \leq 100000$。
• $0 \leq a_{i}, b_{i} \leq 2 \cdot N-1$。
• 所有 $a_{i}$ 和 $b_{i}$ 都是唯一的。

若第一行输出的最小步骤数 $K$ 值正确，而给出的方案不正确，程序可获 $50\%$ 的分数。

详细子任务附加限制及分值如下表所示。