题目描述

题目译自 XV OI Olimpiada Informatyczna – III etap Trójkąty

我们有 $n$ $(n \geq 3)$ 个平面上的点，这些点两两不同。可以形成 $\frac{n \cdot (n-1) \cdot (n-2)}{6}$ 个三角形，这些三角形的顶点是从这些点中选出的两两不同的三点（包括退化三角形，即三个顶点共线的三角形）。

我们希望计算所有这些三角形面积的总和。

属于多个三角形的平面区域会被多次计入面积。我们假设退化三角形的面积为零。

编写一个程序，完成以下功能：

• 从标准输入读取平面上给定点的坐标，
• 计算所有以给定点为顶点的三角形面积总和，
• 将结果输出到标准输出。

输入格式

输入数据的第一行包含一个整数 $n$ $(3 \leq n \leq 3000)$，表示选定点的数量。

接下来的 $n$ 行，每行包含两个整数 $x_{i}$ 和 $y_{i}$ $(0 \leq x_{i}, y_{i} \leq 10000)$，用单个空格分隔，表示第 $i$ $(i=1,2,\ldots,n)$ 个点的坐标。输入中没有重复的有序坐标对。

输出格式

输出应包含一行，且仅一行，包含一个实数，表示所有以给定点为顶点的三角形面积总和。结果应精确到小数点后一位，且与实际值的误差不应超过 $0.1$。

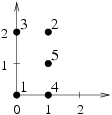
5
0 0
1 2
0 2
1 0
1 1

7.0