题目描述

题目译自 Open Olympiad in Informatics 2025 Day2 T1 「Сильная связность наносит ответный удар / Strong Connectivity Strikes Back」。

在有向图中，如果从顶点 $u$ 到顶点 $v$ 存在一条路径，同时从顶点 $v$ 到顶点 $u$ 也存在一条路径，则称顶点 $u$ 和 $v$ 是强连通的。注意到，如果 $u$ 和 $v$ 强连通，且 $v$ 和 $w$ 强连通，则 $u$ 和 $w$ 也是强连通的。因此，图的顶点可以被分成若干集合——强连通分量。属于某个强连通分量的顶点，与该分量内的所有顶点（包括自身）强连通，而与分量外的顶点不强连通。

在图论课上，爱丽丝在黑板上画了一个包含 $n$ 个顶点的有向图，并标注了其强连通分量。课间休息时，鲍勃决定捉弄爱丽丝，擦除图中某些边的方向。他希望在休息结束后，爱丽丝能够根据剩余的边和强连通分量的划分，唯一地恢复被擦除的方向。

请帮助鲍勃，计算出他最多可以在多少条边上擦除方向，以及有多少种方式可以做到这一点。

更形式化地，求图中边的子集 $A$ 的最大大小，使得满足以下性质：如果擦除子集 $A$ 中边的方向，则根据原来的强连通分量信息和未被擦除方向的边，可以唯一地恢复子集 $A$ 中边的方向，使得强连通分量保持不变。

由于最大子集的数量可能非常大，请输出其对 $10^{9} + 7$ 取模的结果。

如果解决方案正确计算了最大子集 $A$ 的大小，但未能正确计算出这样的子集数量，将获得部分分数。

输入格式

第一行包含三个整数 $n, m, g$ $(2 \leq n \leq 2000, 1 \leq m \leq 2000, 0 \leq g \leq 7)$，分别表示图的顶点数、边数和子任务编号。

接下来的 $m$ 行，每行包含两个整数 $u_i$ 和 $v_i$ $(1 \leq u_i, v_i \leq n, u_i \neq v_i)$，表示第 $i$ 条边的起点和终点顶点编号。

保证对于任意 $1 \leq i, j \leq n$，$(u_i, v_i) \neq (u_j, v_j)$ 且 $(u_i, v_i) \neq (v_j, u_j)$，即任意两个顶点之间最多有一条边，不论方向如何。

输出格式

第一行输出一个整数，即可以擦除方向的最大边子集的大小。

第二行输出一个整数，即这样的最大子集数量对 $10^{9} + 7$ 取模的结果。如果你不打算计算子集数量，可以在第二行输出任意一个 $-1$ 到 $10^{9} + 6$ 之间的数字，此时你的解决方案将获得部分分数。

注意，如果第二行没有输出任何数字，将导致「答案错误」判定，并在此测试点中得 $0$ 分，即使子集大小正确也无济于事。

5 6 0
1 2
1 5
2 3
3 4
3 5
4 2

3
3

示例图中标注了强连通分量：

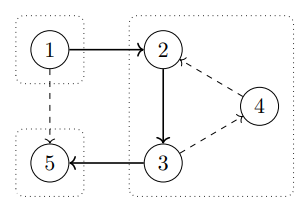
在用虚线标注的边上可以擦除方向。确实，边 $(1, 5)$ 不能反向，否则顶点 $1$、$2$、$3$ 和 $5$ 将处于同一强连通分量。边 $(3, 4)$ 和 $(4, 2)$ 也不能反向，否则顶点 $2$、$3$ 和 $4$ 将不再处于同一强连通分量。

以下是一个不正确的选择子集方式：

在此不能擦除用粗虚线标注的边的方向。例如，如果将边 $(1, 2)$ 和 $(1, 5)$ 的方向反转，将得到一个具有相同强连通分量划分的图。

可以证明，无法在 $4$ 条边上擦除方向，因此答案为 $3$。

数据范围与提示

详细子任务附加限制及分值如下表所示。其中子任务 $0$ 是样例。