题目描述

题目译自 Open Olympiad in Informatics 2016 Day2 T4 「Фото от пилота / See the Sights on the Flights」。

迪玛是一位建筑师，同时也是一位摄影师。他经常周游世界，拍摄当地的标志性建筑，如大本钟和其他令人印象深刻的建筑物。

这一次，迪玛来到了以地铁系统闻名的伯利安迪亚。地铁系统由 $n$ 条线路组成，每条线路在城市地图上表示为一条直线。每两条地铁线路的交点处都设有车站，这些车站的地上亭子被认定为国家建筑遗产。迪玛一在智能手机屏幕上看到这些亭子，就立刻燃起了拍摄它们的欲望。

为此，他决定使用航线直升机进行拍摄。直升机公司提供 $t$ 条航线，每条航线也是一条直线。迪玛可以在航线的任意点进行拍摄，但距离车站越近，照片细节越丰富，在社交媒体上获得的点赞数就越多。因此，他需要你的帮助。

给定 $n$ 条直线表示地铁线路，以及 $t$ 条直线表示可用的直升机航线，迪玛希望你为每条航线计算到离它最近的车站的距离。

保证任意两条地铁线路不重合且任意两条线路都会相交，同时任意两条航线都会相交，且任意航线与任意地铁线路都会相交。

输入格式

第一行包含两个整数 $n$ 和 $t$ $(2 \leq n \leq 100000, 1 \leq t \leq 20)$，分别表示地铁线路数量和可用航线数量。

接下来的 $n$ 行，每行包含三个整数 $a_i, b_i, c_i$ $(|a_i|, |b_i| \leq 10000, a_i^2 + b_i^2 > 0, |c_i| \leq 10^{8})$，描述地铁线路。每条线路表示为直线方程 $a_i \cdot x + b_i \cdot y + c_i = 0$。

再接下来的 $t$ 行，每行包含三个整数 $u_i, v_i, w_i$ $(|u_i|, |v_i| \leq 10000, u_i^2 + v_i^2 > 0, |w_i| \leq 10^{8})$，描述直升机航线。每条航线同样表示为直线方程 $u_i \cdot x + v_i \cdot y + w_i = 0$。

输出格式

对于每条航线，输出一个实数，表示第 $i$ 条直升机航线到距离最近的车站的距离。答案将被认为是正确的，如果其与标准答案的绝对误差或相对误差不超过 $10^{-9}$，即 $\frac{|p - j|}{\max(1, j)} \leq 10^{-9}$，其中 $p$ 是参赛者的答案，$j$ 是标准答案。

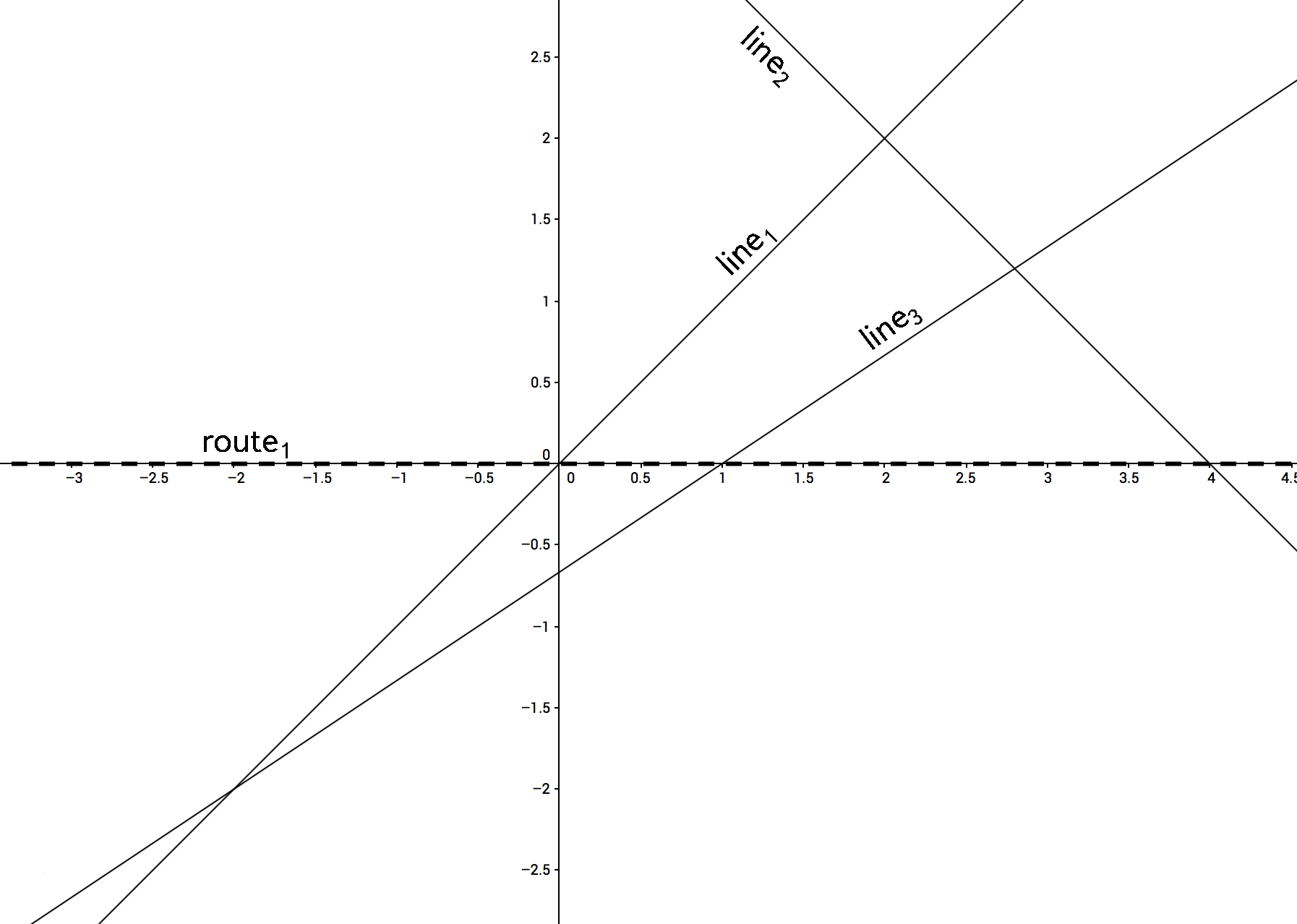
3 1
1 -1 0
1 1 -4
4 -6 -4
0 1 0

1.2

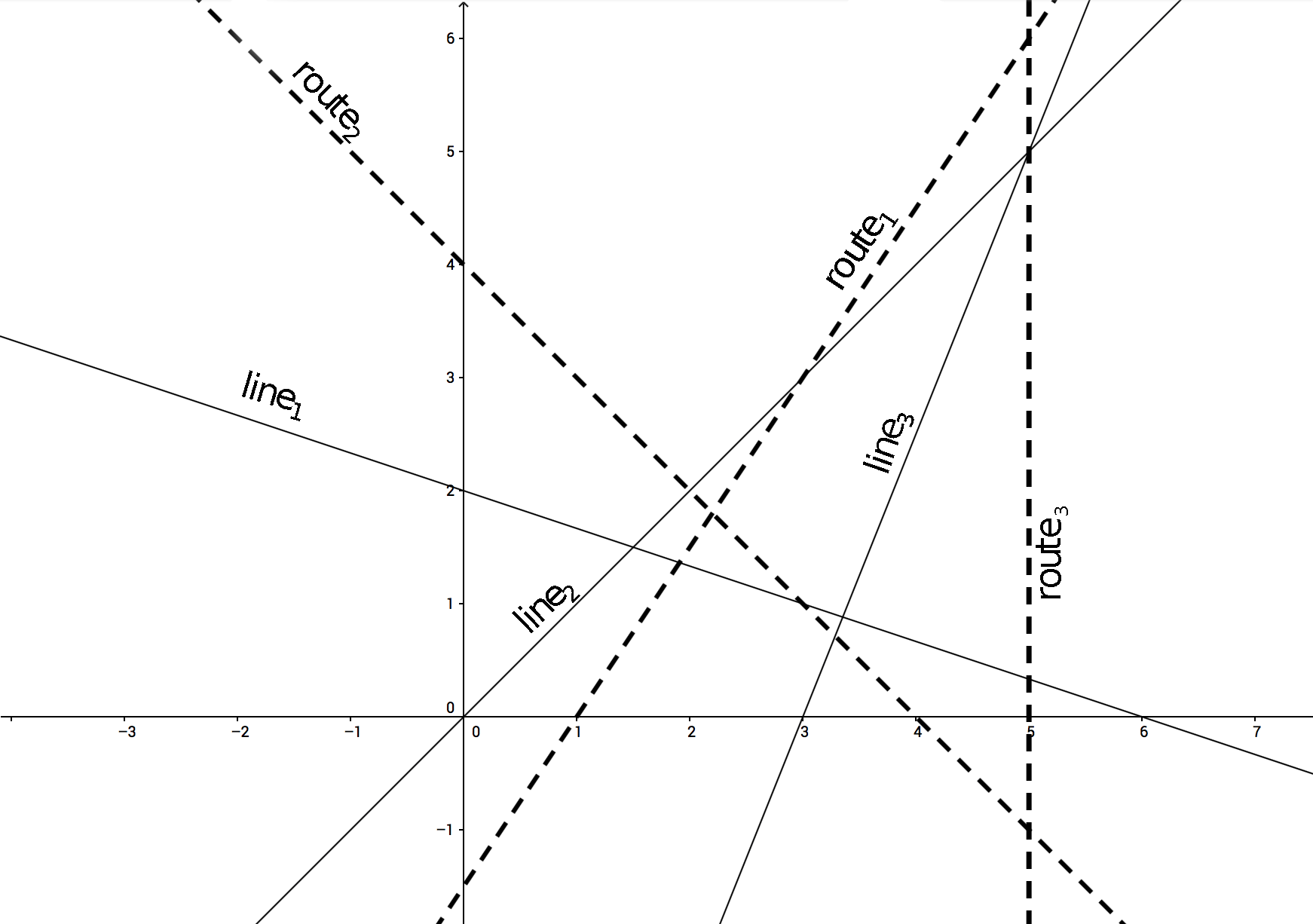
3 3
1 3 -6
-1 1 0
-5 2 15
3 -2 -3
-1 -1 4
1 0 -5

0.41602514717
0.16637806616
0.0

数据范围与提示

详细子任务附加限制及分值如下表所示。其中子任务 $0$ 是样例。