题目描述

题目译自 Ukrainian Olympiads in Informatics 2018 Stage 4 Day2 T4. Оля та площина

小女孩奥莉娅是一个完美的榜样：她每天都在解决各种问题。然而，在家里几乎无法专心学习，因为她有一只淘气的猫科斯蒂安，每次有机会就会捣乱。因此，当奥莉娅在生日收到一块巨大的白色笛卡尔平面作为笔记工具时，科斯蒂安立刻打算破坏这个美妙的礼物。

这块平面是一个白色的正方形，左下角坐标为 $(0, 0)$，右上角坐标为 $(N, N)$。为了方便，奥莉娅在平面的每个角落（即点 $(0, 0)$、$(N, 0)$、$(0, N)$ 和 $(N, N)$）各放置了一瓶墨水，然后开始编写复杂的竞赛题目。

当奥莉娅正在解决一道题目时，科斯蒂安可能会走过来「意外」打翻任意一瓶墨水，于是平面上的一个矩形区域（其对角线端点为放置墨水的点和点 $(x, y)$）就会被无可挽回地弄脏，全部被染成黑色。奥莉娅当然会有些生气，但也没办法——她只能重新装满墨水瓶，继续编写竞赛题目。而此时，科斯蒂安又可能再次打翻墨水，弄脏平面的另一部分区域。

有时，当奥莉娅遇到特别困难的题目时，她会决定在平面上的某个区域记下自己的想法。她总是选择一个与坐标轴平行的矩形区域作为笔记区域。当然，奥莉娅需要知道她选择的区域中有多大面积被墨水弄脏。由于她忙于解决竞赛题目，你需要帮助她完成这项任务。

编写一个程序，根据竞赛期间发生的事件信息，帮助奥莉娅计算平面中被弄脏的区域的面积。

输入格式

输入文件的第一行包含两个整数 $N$ 和 $Q$ $(1 \leq N, Q \leq 10^5)$，分别表示平面的尺寸和竞赛期间发生的事件数量。

接下来有 $Q$ 行描述事件。每行以一个数字 $t$ 开头，表示事件类型。如果 $1 \leq t \leq 4$，表示科斯蒂安打翻了对应的墨水瓶。此时，接下来有两个数字 $x$ 和 $y$ $(0 \leq x, y \leq N)$，表示将被染成黑色的矩形区域的对角线端点。

第一瓶墨水位于左下角，第二瓶位于右下角，第三瓶位于左上角，第四瓶位于右上角。

如果 $t$ 等于 $0$，则接下来有 $4$ 个整数 $x_1, y_1, x_2, y_2$ $(0 \leq x_1 < x_2 \leq N, 0 \leq y_1 < y_2 \leq N)$，表示奥莉娅选择了一个与坐标轴平行的矩形区域，其对角线端点为 $(x_1, y_1)$ 和 $(x_2, y_2)$。

保证输入文件中至少包含一个类型为 $0$ 的事件，且猫弄脏的矩形区域面积不为零。

输出格式

对于每个类型为 $0$ 的查询，在输出文件中单独一行输出一个整数，表示奥莉娅选择的矩形区域中被猫弄脏的部分的面积。查询的答案需按输入数据中的顺序输出。

8 5
1 2 4
2 0 1
3 3 3
4 6 6
0 1 2 7 7

10

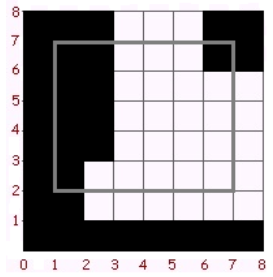
以下是第一个样例中平面的一部分示意图。黑色矩形是被猫弄脏的平面部分，灰色区域是奥莉娅为笔记选择的区域。

6 8
1 1 1
4 5 5
0 0 0 6 6
3 3 3
2 3 3
0 1 1 5 5
2 1 5
0 0 2 6 5

2
8
17

数据范围与提示

详细子任务附加限制及分值如下表所示：