题目描述

注意：在 LibreOJ 上，由于语言限制，目前只支持以下语言的提交：

• C++（标准为 C++ 11 及以上）

请在提交源代码前添加 #include "dungeons.h"。

Robert 正在设计一款新的电脑游戏。游戏中有一位英雄、$n$ 个敌人和 $n + 1$ 个地牢。敌人从 $0$ 到 $n - 1$ 编号，地牢从 $0$ 到 $n$ 编号。敌人 $i$（$0 \le i \le n - 1$）处在地牢 $i$，其能力值为 $s[i]$。地牢 $n$ 里没有敌人。

英雄一开始进入地牢 $x$，初始能力值为 $z$。每次英雄进入地牢 $i$（$0 \le i \le n - 1$）时，都需要面对敌人 $i$，且会发生以下情况中的一种：

• 如果英雄的能力值大于等于敌人 $i$ 的能力值 $s[i]$，那么英雄会胜出。这使得英雄的能力值增加 $s[i]$（$s[i] \ge 1$）。这种情况下，下一步英雄将会进入地牢 $w[i]$（$w[i] > i$）。

• 否则英雄会战败，这使得英雄的能力值增加 $p[i]$（$p[i] \ge 1$）。在这种情况下，下一步英雄将会进入地牢 $l[i]$。

注意 $p[i]$ 可能会小于、等于、大于 $s[i]$，$l[i]$ 可能会小于、等于、大于 $i$。无论对战结果如何，敌人 $i$ 始终处在地牢 $i$，且能力值为 $s[i]$。

当英雄进入地牢 $n$ 的时候，游戏结束。可以看出无论英雄的起始地牢和初始能力值如何，游戏一定会在有限次对战之后结束。

Robert 希望你通过 $q$ 次模拟来对游戏进行测试。对于每次模拟，Robert 输入英雄的起始地牢 $x$ 和初始能力值 $z$。你需要做的是对于每次模拟给出游戏结束时英雄的能力值。

实现细节

你要实现以下函数：

void init(int n, int[] s, int[] p, int[] w, int[] l)

• $n$：敌人的数量。
• $s$、 $p$、 $w$、 $l$：长度为 $n$ 的序列。对于每一个 $i$（$0 \le i \le n - 1$）：
  • $s[i]$ 是敌人 $i$ 的能力值，也是击败敌人 $i$ 后英雄增加的能力值。
  • $p[i]$ 是英雄被敌人 $i$ 击败后增加的能力值。
  • $w[i]$ 是英雄击败敌人 $i$ 后进入的下一个地牢的编号。
  • $l[i]$ 是英雄被敌人 $i$ 击败后进入的下一个地牢的编号。
• 恰好调用此函数一次，且发生在任何对如下的 simulate 函数的调用之前。

int64 simulate(int x, int z)

• $x$：英雄的起始地牢编号。
• $z$：英雄的初始能力值。
• 假设英雄的起始地牢编号为 $x$，初始能力值为 $z$，函数的返回值是相应情况下游戏结束时英雄的能力值。
• 恰好调用此函数 $q$ 次。

评测程序示例

评测程序示例以如下格式读取输入数据：

• 第 $1$ 行：$n \; q$
• 第 $2$ 行：$s[0] \; s[1] \; \ldots \; s[n − 1]$
• 第 $3$ 行：$p[0] \; p[1] \; \ldots \; p[n − 1]$
• 第 $4$ 行：$w[0] \; w[1] \; \ldots \; w[n − 1]$
• 第 $5$ 行：$l[0] \; l[1] \; \ldots \; l[n − 1]$
• 第 $6 + i$ 行（$0 \le i \le q - 1$）：$x \; z$，是第 $i$ 次调用 simulate 的参数。

评测程序示例以如下格式打印你的答案：

• 第 $1 + i$ 行（$0 \le i \le q - 1$）：第 $i$ 次调用 simulate 的返回值。

3 2
2 6 9
3 1 2
2 2 3
1 0 1
0 1
2 3

24
25

考虑以下调用：

init(3, [2, 6, 9], [3, 1, 2], [2, 2, 3], [1, 0, 1])

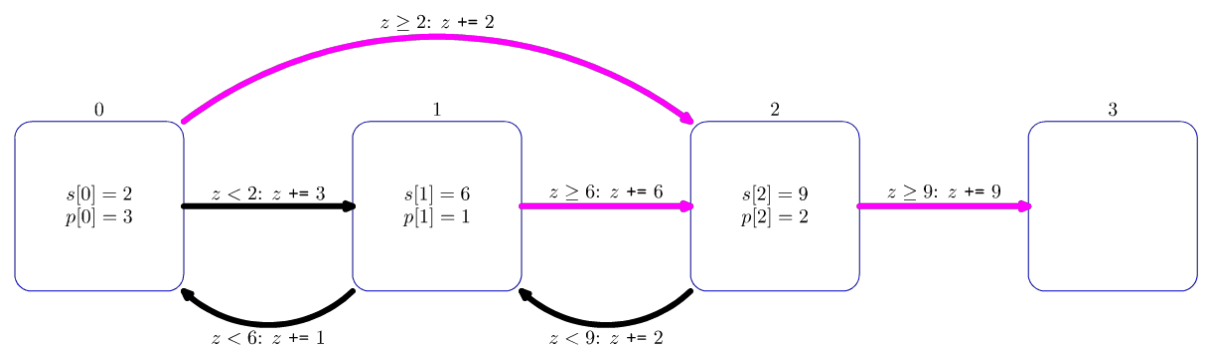
上图对应这次的 init 调用。每一个正方形都代表了一个地牢。对于所有存在敌人的地牢，$s[i]$、$p[i]$ 对应的值都已经在正方形内表示出来了。红色箭头展示了英雄战胜敌人后游戏状态的变化，黑色箭头展示了英雄战败后游戏状态的变化。

这时如果调用 simulate(0, 1)，游戏会以如下方式进行：

因此，simulate(0, 1) 的返回值应该是 $24$。

这时如果调用 simulate(2, 3)，游戏会以如下方式进行：

因此，simulate(2, 3) 的返回值应该是 $25$。

数据范围与提示

对于所有数据：

• $1 \le n \le 400 \, 000$
• $1 \le q \le 50 \, 000$
• $1 \le s[i], p[i] \le {10}^7$（对于所有的 $0 \le i \le n - 1$）
• $0 \le l[i], w[i] \le n$（对于所有的 $0 \le i \le n - 1$）
• $w[i] > i$（对于所有的 $0 \le i \le n - 1$）
• $0 \le x \le n - 1$
• $1 \le z \le {10}^7$