Description

Anna and Beka are at different points on a coordinate line, planning to meet. Their only means of movement is through the use of teleporters.

There are $N$ teleporters, with the i-th teleporter located at coordinate $c[i]$ and operating at a frequency denoted as $f[i]$. However, not all of them are currently available; only those within the frequency range $[L, R]$ can be used.

Using a teleporter takes a minute and transports its user to a coordinate that is a reflection of the original coordinate around the teleporters location. In other words, if the original coordinate was $x_1$, then after using teleporter $i$, the resulting coordinate $x_2$ will satisfy the equation $(x_1 + x_2)/2 = c[i]$.

Each minute, Anna and Beka must use one of the available teleporters (not necessarily different ones). They will communicate during teleportation and experience discomfort equal to the absolute difference of the frequencies of the teleporters they are using. The overall difficulty of the travel is defined as the maximum discomfort they have experienced.

You will be asked about $Q$ different scenarios, and for each one, your task is to determine whether Anna and Beka can ever meet using available teleporters, and if so, what the minimum possible travel difficulty is. A single scenario is described by four integers:

• $A$: Anna's starting coordinate
• $B$: Beka's starting coordinate
• $L$: The minimum frequency of the available teleporters
• $R$ : The maximum frequency of the available teleporters

For each scenario, print the minimum travel difficulty if they can meet and $-1$ otherwise. Please note that the total travel time is irrelevant for the purposes of this task.

Input Format

The first line contains two integers: $N$ and $Q$.

The second line contains $N$ integers: $c[1], c[2], \ldots , c[N]$.

The third line contains $N$ integers: $f[1], f[2], \ldots , f[N]$.

Each of the following $Q$ lines describes one scenario with four integers: $A$, $B$, $L$ and $R$ $(A \neq B)$.

Output Format

Print $Q$ space-separated integers in a single line: answers to the scenarios $1, 2, \ldots ,Q$.

4 3
4 6 8 10
7 1 9 4
3 11 1 50
3 11 1 5
5 7 1 1

2 3 -1

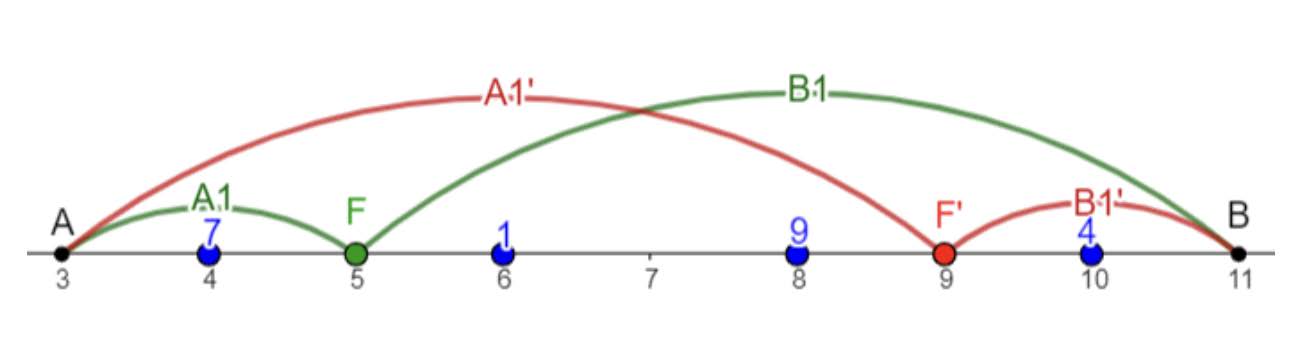
In the first scenario, if Anna uses teleporter $2$ and Beka uses teleporter $4$, they will meet at coordinate $9$ with a discomfort of $|1 - 4| = 3$.

A better solution is if Anna uses teleporter $1$ and Beka uses teleporter $3$ instead; in this case, they meet at $F = 5$ and experience a discomfort of $|7 - 9| = 2$.

In the second scenario, the better option is no longer available due to restriction on the frequency range.

In the third scenario, there is only one available teleporter, and meeting isn't possible.

3 3
-2 1 -1
10 1 3
-6 6 20 20
-6 6 0 20
-6 6 2 20

-1 2 7

Coordinates can be negative.

Constraints

• $2 \leq N \leq 50\,000$
• $1 \leq Q \leq 50\,000$
• $1 \leq f [i] \leq 10^9$
• $-10^9 \leq c[i], A, B \leq 10^9$
• $1 \leq L \leq R \leq 10$

Subtasks

1. (11 points) $N , Q \leq 10$; $|c[i]|, f [i] \leq 50$ for each $1 \leq i \leq N$.
2. (10 points) $N \leq 100$; $L = 1$; $R = 100$; $|c[i]|, f[i] \leq 100$ for each $1 \leq i \leq N$.
3. (5 points) $N = 2$; $L = 1$; $R = 10^9$
4. (9 points) $N \leq 1\,000$; $L = 1$; $R = 10^9$; $f[i] = 1$ for each $1 \leq i \leq N$.
5. (6 points) $L = 1$; $R = 10^9$; $f[i] = 1$ for each $1 \leq i \leq N$.
6. (7 points) $N \leq 1\,000$; $L = 1$; $R = 10^9$
7. (17 points) $L = 1$; $R = 10^9$
8. (8 points) $L = 1$
9. (14 points) $N , Q \leq 20\,000$
10. (13 points) No additional constraints.