Description

You are given a rooted tree consisting of $N$ vertices, along with integers $R$ and $M$. The vertices are numbered from $1$ to $N$, with vertex $1$ as a root. Each of the other vertices has a single parent in the tree.

If a vertex $s$ is chosen, it becomes infected along with all its descendants (i.e. vertices that can be reached by following edges downward from $s$) at a distance of $R$ or less, where distance is calculated as the number of edges between vertices. A vertex $u$ is considered reachable from vertex $v$ if and only if neither of them is infected, and the number of infected vertices on the path between them does not exceed $M$.

For each possible chosen vertex $s$ ($1 \leq s \leq N$), you must calculate the number of vertex pairs $(u, v)$ such that $1 \leq u < v \leq N$ and $u$ is reachable from $v$ (and vice versa).

Input Format

The first line contains three integers: $N$, $R$ and $M$.

The second line contains $N - 1$ integers: $p[2], p[3], \ldots ,p[N]$, the parents of the vertices $2, 3, \ldots ,N$, respectively.

Output Format

Print $N$ lines with single integer each: $s$-th line should contain required number of pairs when the chosen vertex is $s$.

It's not recommended to use std::endl for outputting newline symbols. Instead, consider using '\n' for better performance.

13 2 2
1 2 3 4 3 6 6 8 2 10 11 1

16
4
15
55
66
36
66
55
66
45
55
66
66

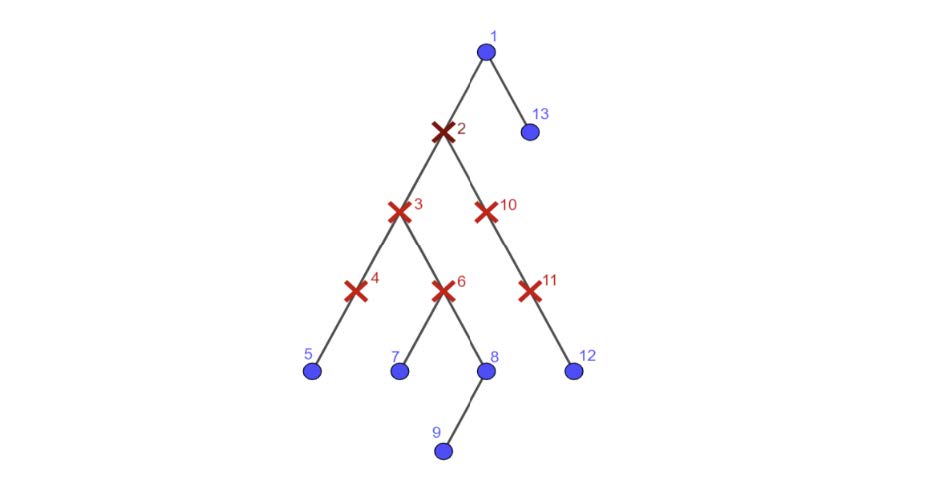
The image above corresponds to $s = 2$.

The reachable pairs are: $(1,13), (7,8), (7,9), (8,9)$.

This list doesn't include the pair $(1,2)$ since vertex $2$ is infected. Similarly, the pair $(1,5)$ is absent since the path between $1$ and $5$ has three infected vertices ($2$, $3$ and $4$).

3 0 1
1 2

1
1
1

Constraints

• $2 \leq N \leq 500\,000$
• $1 \leq p[i] < i$ (for each $2 \leq i \leq N$)
• $0 \leq R \leq N - 1$
• $0 \leq M \leq 2 \times R + 1$

Subtasks

1. (20 points) $N \leq 300$
2. (14 points) $R = 0$
3. (15 points) $M = 2 \times R + 1$
4. (10 points) $M = 2 \times R - 1$
5. (16 points) $N \leq 5\,000$
6. (25 points) No additional constraints.