Description

Maribor has just been visited by aliens! They share with you their technology and their history.

There are $N+1$ planets, indexed from $0$ to $N$, where Earth has index $N$. Every planet has a unique population count ($P[i]$ for the $i$-th planet, $i \in\{0, \ldots, N\}$). The planets are connected with $N$ bidirectional portals in such a way that you can travel between any two planets using only these portals. Portal $i$ ($i \in\{0, \ldots, N-1\}$) connects planets $U[i]$ and $V[i]$. The distance between two planets is the least number of portals required to travel between them.

You start from Earth and want to make excursion and visit $K$ other planets - $A[0], A[1], \ldots$, $A[K-1]$. These are called planets of origin. You also know that each planet of origin and Earth have only one portal connected to it. Your excursion is a shortest route that starts from Earth and visits all planets of origin and also all the planets along the way. Let $S$ be the set of all visited planets.

Now the aliens decided to test whether Earth is worthy to join their supercivilization by asking you $Q$ questions of two types.

• Type $1$: What is the size of the set $S$?
• Type $2$: They pick a planet $x$ from $S$, a distance $d$, and a number $r$. They ask you what is the $r$-th smallest planet by population count among the planets at distance $d$ from $x$. (For instance, if $r=1$, this is the planet with the least population count. This planet can, but does not have to belong to the set $S$.).

There is exactly one query of type $1$.

Input format

Line 1: $N, K, Q$.

Line 2: $P[0], \ldots, P[N]$.

Line 3: $A[0], \ldots, A[K-1]$.

The $i$-th $(i \in\{0, \ldots, N-1\})$ of the following $N$ lines: $U[i]$ and $V[i]$.

The following $Q$ lines satisfy one of these formats:

• $1$ (a query of type $1$)
• $2\,x\,d\,r$ (a query of type $2$)

Output

For every query print the answer in one line. Either the number of planets visited during the excursion, or the $r$-th planet by population from the planets at distance $d$ from $x$.

Input bounds

• $1 \leq N \leq 100000 ; 1 \leq K \leq 10 ; 1 \leq Q \leq 100000$.
• for $0 \leq i \leq N$ it holds $1 \leq P[i] \leq 10^{9}$. All $P[i]$ are unique.
• for $0 \leq i \leq K-1$ it holds $0 \leq A[i] \leq N-1$.
• for $0 \leq i \leq N-1$ it holds $0 \leq U[i], V[i] \leq N$
• The $K$ planets of origin and the planet Earth have exactly one portal connected to them.
• For each query, a value $1 \leq t \leq 2$ is given. When $t=2$, additional values $x, d$ and $r$ are given. It holds that $x \in S, d \geq 1$, and $r \geq 1$.
• It is guaranteed that there are at least $r$ planets at a distance $d$ from planet $x$.

Subtasks

1. (3 points) $Q=1$.
2. (14 points) $N \leq 2000, Q \leq 2000$.
3. (21 points) $K=1$.
4. (12 points) $N \leq 10000$.
5. (13 points) $Q \leq 10000$.
6. (37 points) No additional constraints.

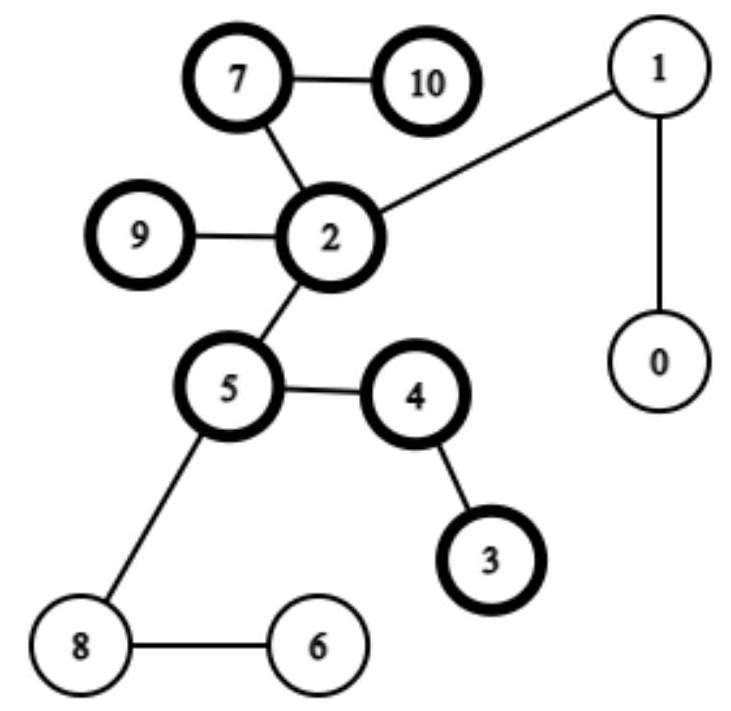
5 1 5
8 7 9 4 16 12
1
0 4
3 1
2 4
5 4
4 3
1
2 4 2 1
2 3 2 1
2 4 1 3
2 5 2 3

4
1
0
2
2

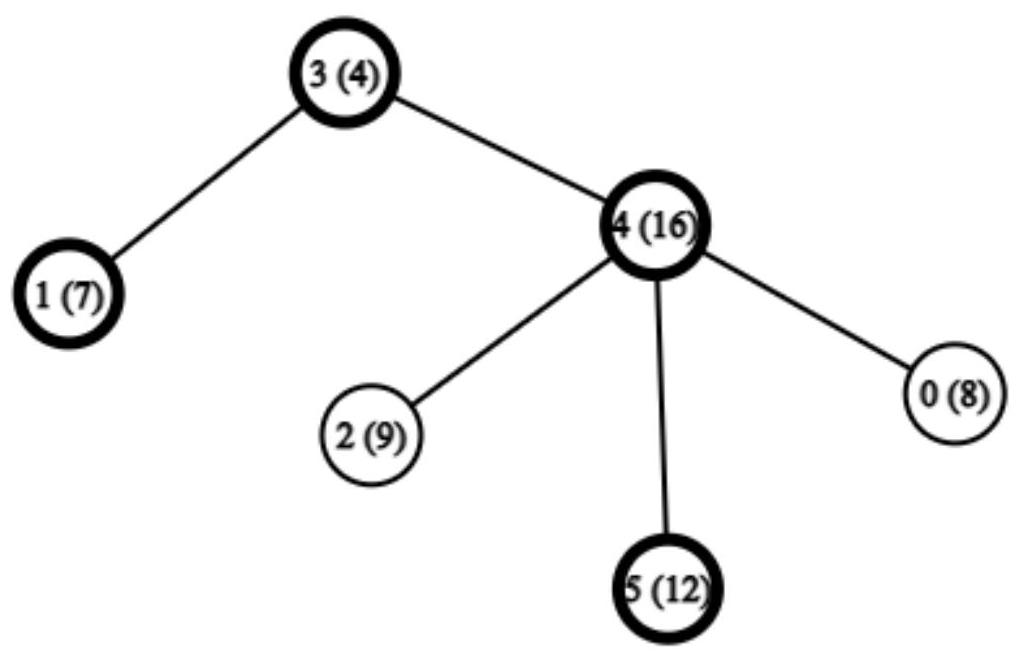
There is one planet of origin, and we visit the planets $S=\{1,3,4,5\}$ during the excursion. The queries of type $2$ are:

• $x=4, d=2, r=1$
• At distance $2$ from planet $4$, there is only the planet $1$.
• $x=3, d=2, r=1$
• At distance $2$ from planet $3$, there are planets $0,2,$ and $5$. Among them, planet $0$ has the lowest population count.
• $x=4, d=1, r=3$
• At distance $1$ from planet $4$, there are the planets $0,2,3,$ and $5$, and their order by population is $3,0,2,5$. The third among them is planet $2$.
• $x=5, d=2, r=3$
• At distance $2$ from planet $5$, there are planets $0,2,$ and $3$, and their order by population is $3,0,2$. The third among them is planet $2$.

10 2 11
1 2 3 4 5 6 7 8 9 10 11
9 3
5 8
2 7
3 4
6 8
0 1
2 9
5 2
4 5
7 10
1 2
1
2 5 1 2
2 5 2 2
2 5 2 3
2 5 2 4
2 9 3 2
2 9 3 3
2 9 4 1
2 2 1 3
2 2 2 4
2 2 3 1

7
4
3
6
7
4
8
3
7
10
3