题目描述

每年，ICPC（国际大学生程序设计竞赛）都会吸引众多赞助商的支持。由于愉快的赞助商意味着愉快的比赛，我们计划在比赛场地的一侧设置一块长长的广告牌，以便我们可爱的赞助商能够在此展示他们的广告。

总共有 $n$ 位出色的赞助商，为了公平起见，我们希望将广告牌的总面积均分给每位赞助商，每人得到 $1/n$ 的面积。然而，问题在于每位杰出的赞助商对广告牌不同位置的价值评估可能有所不同。例如，有些赞助商希望将广告放置在比赛场地的入口附近，这样所有参赛者进入时都能确保看到他们的广告；而另一些赞助商可能更倾向于将广告放在中间位置，因为那里更有可能出现在直播画面中。（别问我们如果入口就在中间会怎样，这只是个例子！）

在与所有亲切的赞助商沟通后，ICPC 工作人员发现每位赞助商的偏好值可以用一个连续的分段线性函数来建模，这些价值函数的定义域是广告牌的长度。基于这些信息，ICPC 工作人员希望将广告牌分割成 $n$ 个部分，并分配给 $n$ 位赞助商，确保每位优秀的赞助商从自己的角度看，至少能获得广告牌总价值的 $1/n$。也就是说，每个赞助商所分配到的部分，其价值函数下的面积必须至少是他们自己价值函数总面积的 $1/n$。

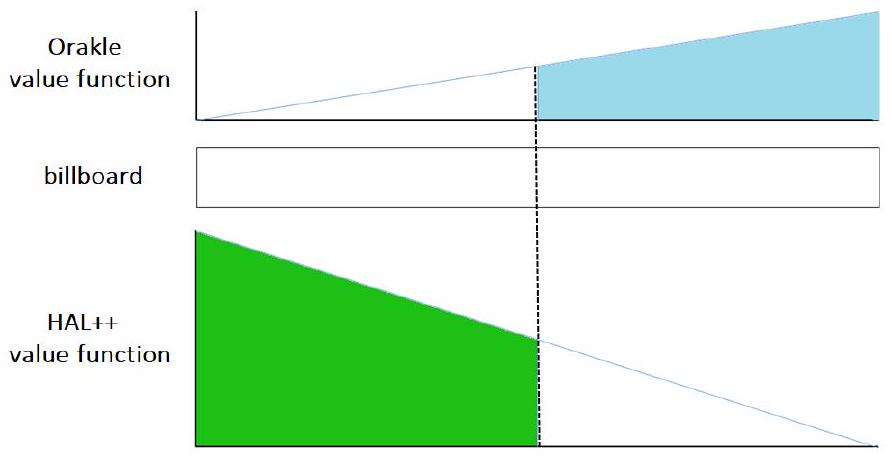
图 A.1 展示了一个简单的例子。广告牌长度为 $10$，有两家赞助商——Orakle Software 和 Hal++，两者的价值函数都只有一段。Orakle 的价值函数显示，该公司越来越偏好广告牌从左到右的部分，而 Hal++ 的价值函数则显示相反的偏好。每个函数下的面积代表从各自赞助商角度看广告牌的总价值。图中所示的蓝色和绿色区域均大于各自总面积的一半，因此在广告牌中间（虚线处）分割是一个合法的方案，最终广告牌如图 A.2 所示。注意，还有许多其他分割方式也是可行的（例如在 $4$ 或 $6$ 处分割也合法，只要广告牌的部分分配给了正确的赞助商）。

输入格式

第一行包含两个整数：$n$ $(1 \leq n \leq 5\,000)$，表示 ICPC 拥有的杰出赞助商数量（编号从 $1$ 到 $n$）；以及 $l$ ($1 \leq l \leq 10^{6}$)，表示广告牌的长度。

接下来的 $n$ 行，每行开头是一个整数 $m$ $(2 \leq m \leq 5\,000)$，表示定义这位受尊敬赞助商价值函数的点的数量。行内剩余部分包含 $m$ 对整数 $(a_{1}, b_{1}), \ldots, (a_{m}, b_{m})$ （其中 $0 = a_{1} < a_{2} < \ldots < a_{m} = l$，$0 \leq b_{i} \leq 100$），每对整数代表分段线性函数一个段的端点。所有 $m$ 的总和最多为 $500\,000$，且保证每个赞助商至少有一个 $b_{i}$ 为正。

输出格式

输出 $n$ 对数字 $(l_{i}, f_{i})$ $(1 \leq i \leq n)$，表示广告牌在区间 $[l_{i-1}, l_{i}]$ 的部分分配给赞助商 $f_{i}$（其中假定 $l_{0} = 0$，且 $l_{0} < l_{1} < l_{2} < \ldots < l_{n}$，$l_{n}$ 必须等于 $l$）。$f_{i}$ 的值必须是区间 $[1, n]$ 内的整数，且每个整数恰好出现一次，但 $l_{i}$ 可以是实数。如果有多种解决方案，输出任意一种即可。如果无解，则输出 impossible。

注意，你无需优化其他任何内容，只要确保每位赞助商获得至少 $1/n$ 的总面积即可。如果每位赞助商分配到的面积低于其总面积的 $1/n$，但绝对或相对误差不超过 $10^{-8}$，也是可接受的。

2 10
2 0 0 10 5
2 0 10 10 0

5 2
10 1

5 100
5 0 0 10 0 20 1 30 0 100 0
5 0 0 10 0 20 1 30 0 100 0
5 0 0 10 0 20 1 30 0 100 0
5 0 0 10 0 20 1 30 0 100 0
5 0 0 10 0 20 1 30 0 100 0

16.3245553203 1
18.9442719100 2
21.0557280900 3
23.6754446797 4
100 5