题目描述

宾果是一种多人参与的运气游戏。每位玩家会获得一张写有若干数字的卡片，游戏主持人会以随机顺序喊出这些数字。玩家听到自己卡片上的数字时可以将其划掉，最先划掉所有数字的玩家赢得游戏。这种基本版本的游戏以节奏较为缓慢而闻名，玩家除了保持清醒外几乎无需任何特别的行动。

在本题中，我们将分析一个更具动态性的宾果游戏版本，这个版本需要快速反应。在我们的版本——速度宾果中，游戏主持人同样以随机顺序喊出卡片上的数字。然而，每当喊出一个数字时，只有最先做出反应的玩家才能在自己的卡片上划掉这个数字。如果玩家的卡片上有多个相同的数字，每次只能划掉一个。当多位玩家卡片上有相同的数字时，反应速度最快的玩家在赢得速度宾果时会占据优势。但这种优势究竟有多大呢？这就是我们需要你帮助解决的问题。

形式化地讲，有 $n$ 位玩家，每人收到一张卡片，上面有 $k$ 个（不一定互不相同）的数字。玩家 $1$ 的反应速度比玩家 $2$ 快，玩家 $2$ 又比玩家 $3$ 快，以此类推，玩家 $n$ 的反应速度最慢。以下是一个例子，对应于第一个示例输入，其中三位玩家每人收到四个数字：

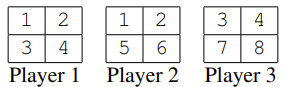
当数字 1 第一次被喊出时，玩家 $1$——由于反应更快——将得以在自己的卡片上划掉它。当数字 1 第二次被喊出时，玩家 $2$ 将得以划掉它。因此，平均而言，我们预期玩家 $1$ 会比玩家 $2$ 和玩家 $3$ 表现更好，因为后两者需要的一些数字会被玩家 $1$ 抢先划掉。然而，由于玩家 $2$ 和玩家 $3$ 的卡片上没有相同的数字，他们的表现互不影响，尽管玩家 $2$ 比玩家 $3$ 反应更快。

假设游戏一直进行到所有玩家都划掉了自己卡片上的所有数字为止，也就是说，直到所有卡片上的 $n \cdot k$ 个数字（包括相应的重复次数）都被喊出。假设数字的喊出顺序是完全随机的，每位玩家最后完成的概率是多少？

输入格式

输入描述了一场速度宾果游戏。第一行包含两个整数 $n$ 和 $k$，分别表示玩家数量和每张卡片上的数字数量 $(1 \leq n \leq 100, 1 \leq k \leq 1\,000)$。接下来有 $n$ 行，每行包含 $k$ 个整数，其中第 $i$ 行的数字表示第 $i$ 位玩家卡片上的数字。所有数字均在 $1$ 到 $10^{9}$ 之间（含边界）。

输出格式

输出 $n$ 行，每行对应一位玩家。第 $i$ 行应包含玩家 $i$ 最后完成的概率。所有数值必须精确到绝对误差不超过 $10^{-6}$。

3 4
1 2 3 4
1 2 5 6
3 4 7 8

0.000000000
0.500000000
0.500000000

4 2
1 2
3 4
10 5
7 8

0.250000000
0.250000000
0.250000000
0.250000000