Description

Relax: No knowledge of thermodynamics is needed to solve this problem.

Maxwell's demon sits in a container of height $h$ and width $2 w$. The container is divided into two adjacent chambers, each of height $h$ and width $w$. An impenetrable wall separates the two chambers, and the demon sits at a fixed position on this center wall.

The chambers contain particles, each particle having a position, a velocity, and a color. When a particle strikes the wall of a chamber, it reflects off the wall with perfect elasticity. Figure H. 1 shows a container with two particles, a blue one in the left chamber and a red one in the right chamber.

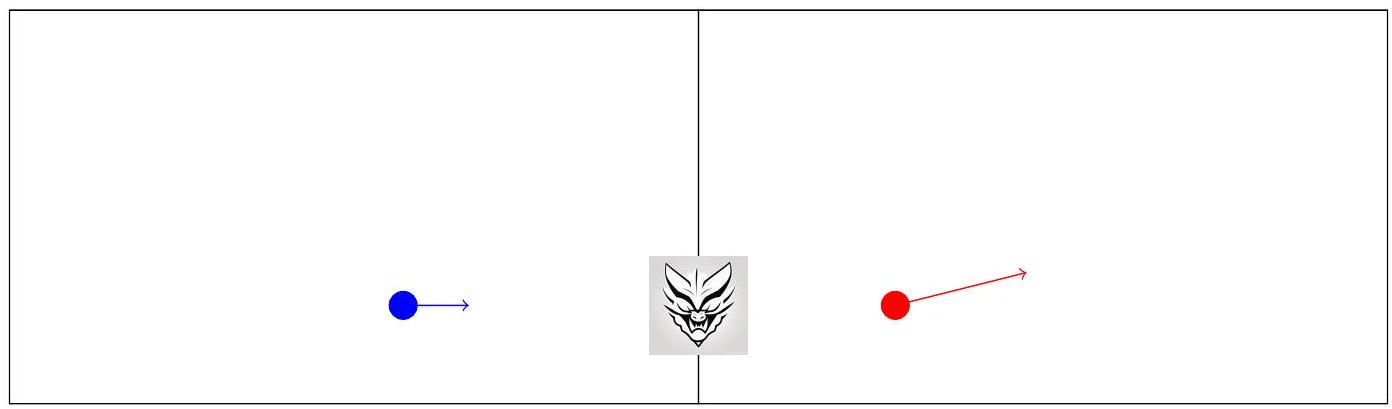
Maxwell's demon seeks to reduce entropy by sorting the particles. It wants all red particles to be in the left chamber and all blue particles to be in the right chamber. To achieve this, it has a special power: it can allow particles to pass through the center wall when they hit the demon's position.

The chamber bottoms lie on the $x$-axis, and their dividing center wall runs along the positive $y$-axis. At any time of the demon's choosing, all particles at the demon's position ($0, d$) will not reflect off the center wall but will instead pass through to the other chamber, maintaining their velocity. The demon can do this whenever and as often as it wants and can also choose not to allow a particle through even though it hits the demon's position. However, if multiple particles are at position ($0, d$) simultaneously, either all such particles pass through the center wall or all particles are reflected.

Help the demon sort the particles and reduce entropy! What is the earliest time when it is possible for all red particles to be in the left chamber and all blue particles to be in the right chamber?

Input

The first line consists of five integers $w, h, d, r, b$, where $w$ and $h$ ($2 \leq w, h \leq 200$) are the width and the height of each chamber, $d$ ($0 \leq d \leq h$) is the $y$-coordinate of the demon's position on the container's center wall, and $r$ and $b$ ($0 \leq r, b$ and $1 \leq r+b \leq 200$) are the number of red and blue particles, respectively.

This is followed by $r+b$ lines, each describing a single particle using four integers $p_{x}, p_{y}, v_{x}, v_{y}$, where $\left(p_{x}, p_{y}\right)$ ($0<\left|p_{x}\right|<w, 0<p_{y}<h$) is the initial position of the particle, and $\left(v_{x}, v_{y}\right)$ ($\left|v_{x}\right|<w, \left|v_{y}\right|<h, (v_{x}, v_{y}) \neq(0,0)$) is the initial velocity of the particle. The first $r$ particles described are red while the remaining are blue.

Output

Output the least amount of time needed for all red particles to be in the left chamber and all blue particles to be in the right chamber. Your answer should have an absolute or relative error of at most $10^{-6}$. If it is impossible for all red particles to be in the left chamber and all blue particles to be in the right chamber within a finite amount of time, output impossible.

7 4 1 1 1
2 1 4 1
-3 1 2 0

24.0

4 4 1 2 2
3 1 2 2
-2 3 -2 -1
3 2 1 -2
-2 2 2 2

impossible